题目内容
6.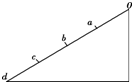 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )| A. | 质点由O到达各点的时间之比ta:tb:tc:td=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 质点通过各点的速率之比va:vb:vc:vd=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| C. | 在斜面上运动的平均速度$\overline{v}$=vb | |
| D. | 在斜面上运动的平均速度$\overline{v}$=$\frac{{v}_{d}}{2}$ |
分析 根据匀变速直线运动的基本公式,结合初速度等于0的特点,由公式逐项分析即可.
解答 解:A、质点块的初速度为0,做匀加速直线运动,则位移:x=$\frac{1}{2}a{t}^{2}$;由于斜面上的四段距离相等,xa:xb:xc:xd=1:2:3:4,所以质点由O到达各点的时间之比ta:tb:tc:td=1:$\sqrt{2}$:$\sqrt{3}$:2.故A正确;
B、根据速度公式:v=at,则:质点通过各点的速率之比va:vb:vc:vd=ta:tb:tc:td=1:$\sqrt{2}$:$\sqrt{3}$:2.故B正确;
C、由于ta:tb:tc:td=1:$\sqrt{2}$:$\sqrt{3}$:2,可知质点到达a的时间是总时间的一半,所以全过程中的平均速度等于a点的平均速度.故C错误;
D、质点块的初速度为0,做匀加速直线运动,由$\overline{v}=\frac{{v}_{0}+{v}_{t}}{2}$可知,质点在斜面上运动的平均速度$\overline{v}$=$\frac{{v}_{d}}{2}$.故D正确.
本题选择不正确的,故选:C
点评 解决本题的关键掌握初速度为0的匀变速运动的两个重要推论,1、某段时间内的平均速度等于中间时刻的瞬时速度.2、从开始计时的连续相等的位移上的时间关系与速度关系都有特定的公式,即:x1:x2:x3:x4=1:$\sqrt{2}$:$\sqrt{3}$:2,v1:v2:v3:v4=1:$\sqrt{2}$:$\sqrt{3}$:2.
这一组的公式最好能记牢.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
17. 如图,斜面体置于水平面上,一横截面为梯形的物块恰能沿斜面匀速下滑.若在物块下滑过程中分别对其施加一个竖直向下的恒力F1或者一垂直斜面向下的恒力F2时,物块仍能沿斜面向下运动,且两种情况下斜面体均静止不动,则下列说法正确的是( )
如图,斜面体置于水平面上,一横截面为梯形的物块恰能沿斜面匀速下滑.若在物块下滑过程中分别对其施加一个竖直向下的恒力F1或者一垂直斜面向下的恒力F2时,物块仍能沿斜面向下运动,且两种情况下斜面体均静止不动,则下列说法正确的是( )
 如图,斜面体置于水平面上,一横截面为梯形的物块恰能沿斜面匀速下滑.若在物块下滑过程中分别对其施加一个竖直向下的恒力F1或者一垂直斜面向下的恒力F2时,物块仍能沿斜面向下运动,且两种情况下斜面体均静止不动,则下列说法正确的是( )
如图,斜面体置于水平面上,一横截面为梯形的物块恰能沿斜面匀速下滑.若在物块下滑过程中分别对其施加一个竖直向下的恒力F1或者一垂直斜面向下的恒力F2时,物块仍能沿斜面向下运动,且两种情况下斜面体均静止不动,则下列说法正确的是( )| A. | 加F1时,物块一定沿斜面匀速下滑 | |
| B. | 加F2时,物块可能沿斜面匀速下滑 | |
| C. | 加F1时,斜面体一定不受地面的摩擦力 | |
| D. | 加F2时,斜面体一定受地面向左的摩擦力 |
11.关于磁场中某点的磁感应强度,下列说法正确地是( )
| A. | 由B=$\frac{F}{IL}$可知,B与F成正比,与IL的乘积成反比 | |
| B. | B的大小与IL的乘积无关,由磁场本身决定 | |
| C. | B的大小和方向处处相同的区域叫匀强磁场 | |
| D. | B的方向与通电导线的受力方向相同 |
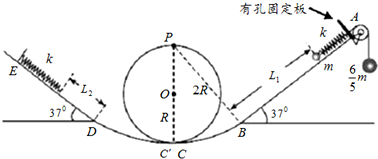
 图是做探究电磁感应的产生条件实验的器材及示意图.
图是做探究电磁感应的产生条件实验的器材及示意图. 如图所示,一竖直放置、半径为R的粗糙半圆形轨道BC与一水平面AB在B点相连,B点为轨道的最低点,C点为轨道的最高点.一质量为m的小球以初速度v0从B点进入竖直圆轨道BC,沿着圆轨道运动并恰好通过最高点C,然后做平抛运动.求:
如图所示,一竖直放置、半径为R的粗糙半圆形轨道BC与一水平面AB在B点相连,B点为轨道的最低点,C点为轨道的最高点.一质量为m的小球以初速度v0从B点进入竖直圆轨道BC,沿着圆轨道运动并恰好通过最高点C,然后做平抛运动.求: