题目内容
11.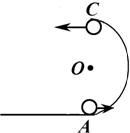 如图所示,竖直的半圆形轨道与水平面相切,轨道半径R=0.2m.质量m=200g的小球以某一速度正对半圆形轨道运动,A、B、C三点分别为圆轨道最低点、与圆心O等高点、最高点.小球过这三点的速度分别为vA=5m/s,vB=4m∠s,vC=3m/s,求:
如图所示,竖直的半圆形轨道与水平面相切,轨道半径R=0.2m.质量m=200g的小球以某一速度正对半圆形轨道运动,A、B、C三点分别为圆轨道最低点、与圆心O等高点、最高点.小球过这三点的速度分别为vA=5m/s,vB=4m∠s,vC=3m/s,求:(1)小球经过这三个位置时对轨道的压力;
(2)小球从C点飞出落到水平面上,其着地点与A点相距多少?(g取10m/s2)
分析 (1)在A、C两点,小球靠重力和弹力的合力提供向心力,在B点,小球靠弹力提供向心力,结合牛顿第二定律求出轨道对小球的弹力大小,从而结合牛顿第三定律得出小球经过这三个位置时对轨道的压力.
(2)根据高度求出平抛运动的时间,结合C点的速度和时间求出着地点与A点的距离.
解答 解:(1)在A点,根据牛顿第二定律得:${N}_{A}-mg=m\frac{{{v}_{A}}^{2}}{R}$,
解得:${N}_{A}=mg+m\frac{{{v}_{A}}^{2}}{R}$=2+0.2×$\frac{25}{0.2}$N=27N.
在B点,根据牛顿第二定律得:${N}_{B}=m\frac{{{v}_{B}}^{2}}{R}$=$0.2×\frac{16}{0.2}$N=16N.
在C点,根据牛顿第二定律得:${N}_{C}+mg=m\frac{{{v}_{C}}^{2}}{R}$,
解得:${N}_{C}=m\frac{{{v}_{C}}^{2}}{R}-mg=0.2×\frac{9}{0.2}-2N=7N$,
根据牛顿第三定律知,小球经过三个位置时对轨道的压力分别为27N、16N、7N.
(2)根据2R=$\frac{1}{2}g{t}^{2}$得:t=$\sqrt{\frac{4R}{g}}=\sqrt{\frac{4×0.2}{10}}s=\frac{\sqrt{2}}{5}s$,
着地点与A点相距为:x=${v}_{C}t=3×\frac{\sqrt{2}}{5}m=\frac{3\sqrt{2}}{5}m$.
答:(1)小球经过三个位置时对轨道的压力分别为27N、16N、7N.
(2)小球从C点飞出落到水平面上,其着地点与A点相距$\frac{3\sqrt{2}}{5}m$.
点评 本题考查了圆周运动和平抛运动的综合运用,知道圆周运动向心力的来源,以及平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 宇宙飞船以周期为T绕地球作近地圆周运动时,由于地球遮挡阳光,会经历“日全食”过程,如图所示.已知地球的半径为R,引力常量为G,地球自转周期为T0.太阳光可看作平行光,宇航员在A点测出的张角为α,则( )
宇宙飞船以周期为T绕地球作近地圆周运动时,由于地球遮挡阳光,会经历“日全食”过程,如图所示.已知地球的半径为R,引力常量为G,地球自转周期为T0.太阳光可看作平行光,宇航员在A点测出的张角为α,则( )| A. | 飞船绕地球运动的线速度为$\frac{2πR}{Tsin(\frac{α}{2})}$ | |
| B. | 一天内飞船经历“日全食”的次数为$\frac{T}{{T}_{0}}$ | |
| C. | 飞船每次经历“日全食”过程的时间为$\frac{aT}{2π}$ | |
| D. | 地球质量为$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}si{n}^{3}(\frac{α}{2})}$ |
| A. | 根据速度定义式$v=\frac{△x}{△t}$,当△t非常非常小时,就可以用$\frac{△x}{△t}$表示物体在t时刻的瞬时速度,这是科学假说法 | |
| B. | 玻璃瓶内装满水,用穿有透明细管的橡皮塞封口.手捏玻璃瓶,细管内液面高度有明显变化,说明玻璃瓶发生形变,该实验采用放大的思想 | |
| C. | 在不需要考虑物体本身的大小和形状时,用质点代替物体的方法,采用了等效替代的思想 | |
| D. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里应用了建立物理模型法 |

| A. | A、B、C三球在运动过程中,加速度都相同 | |
| B. | B球的射程最远,所以最迟落地 | |
| C. | A球的射高最大,所以最迟落地 | |
| D. | A、C两球的水平位移相等,所以两球的水平速度分量相等 |
 如图所示,A、B为平行板电容器的金属板,G为静电计.开始时开关S闭合,静电计指针张开一定角度.下列操作可使指针张开角度增大一些的是( )
如图所示,A、B为平行板电容器的金属板,G为静电计.开始时开关S闭合,静电计指针张开一定角度.下列操作可使指针张开角度增大一些的是( )| A. | 保持开关S闭合,将R上的滑片向右移动 | |
| B. | 保持开关S闭合,将A、B两极板分开一些 | |
| C. | 断开开关S后,将A、B两极板的正对面积减小一些 | |
| D. | 断开开关S后,将A、B两极板分开一些 |