题目内容
8.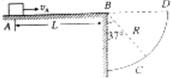 如图所示,水平面AB的右侧有一圆形挡板,圆的半径R=0.16m,B为圆心,BC连线与竖直方向的夹角为37°,可视为质点的滑块以一定的初速度从水平面上的A点沿AB方向运动,恰好落在圆形挡板的C点.已知AB间距为L=2.16m,滑块与水平面间的动摩擦因数μ=0.2,取g=10m/s2,sin37°=0.6.求:
如图所示,水平面AB的右侧有一圆形挡板,圆的半径R=0.16m,B为圆心,BC连线与竖直方向的夹角为37°,可视为质点的滑块以一定的初速度从水平面上的A点沿AB方向运动,恰好落在圆形挡板的C点.已知AB间距为L=2.16m,滑块与水平面间的动摩擦因数μ=0.2,取g=10m/s2,sin37°=0.6.求:(1)滑块到达C点时速度的大小;
(2)滑块在A点速度的大小.
分析 (1)滑块离开B点做平抛运动,根据几何关系求出平抛运动的竖直位移和水平位移,结合竖直位移求出运动的时间,再结合水平位移求出初速度,根据速度时间公式求出竖直分速度,通过平行四边形定则求出滑块到达C点的速度大小.
(2)根据牛顿第二定律求出滑块在水平面上的加速度大小,结合速度位移公式求出滑块在A点的速度大小.
解答 解:(1)滑块离开B点做平抛运动,平抛运动的水平位移为:
x=Rsin37°=0.16×0.6m=0.096m,
平抛运动的竖直位移为:
y=Rcos37°=0.16×0.8m=0.128m,
根据y=$\frac{1}{2}g{t}^{2}$得平抛运动的时间为:
t=$\sqrt{\frac{2y}{g}}=\sqrt{\frac{2×0.128}{10}}s=0.16s$,
则平抛运动的初速度为:${v}_{B}=\frac{x}{t}=\frac{0.096}{0.16}m/s=0.6m/s$,
到达C点的竖直分速度为:vy=gt=10×0.16m/s=1.6m/s,
则C点的速度大小为:${v}_{C}=\sqrt{{{v}_{B}}^{2}+{{v}_{y}}^{2}}$=$\sqrt{0.36+1.{6}^{2}}$≈1.7m/s.
(2)滑块在水平面上做匀减速直线运动加速度大小为:
a=$\frac{μmg}{m}=μg=0.2×10m/{s}^{2}=2m/{s}^{2}$,
根据${{v}_{A}}^{2}-{{v}_{B}}^{2}=2aL$得:${v}_{A}=\sqrt{{{v}_{B}}^{2}+2aL}$=$\sqrt{0.36+2×2×2.16}$m/s=3m/s.
答:(1)滑块到达C点时速度的大小为1.7m/s;
(2)滑块在A点速度的大小为3m/s.
点评 本题考查了平抛运动和直线运动的综合运用,结合平抛运动的规律求出B点的速度是解决本题的关键,对于水平面上的运动,可以根据动力学求解,也可以根据动能定理进行求解.

 如图所示,虚线表示带电粒子在电场中的运动轨迹,电场分布如图,忽略其它力的影响,则( )
如图所示,虚线表示带电粒子在电场中的运动轨迹,电场分布如图,忽略其它力的影响,则( )| A. | A点电势高于B点电势 | |
| B. | A点场强小于B点场强 | |
| C. | 粒子在A点的速度一定大于它在B点的速度 | |
| D. | 粒子一定带正电 |
 如图所示,在x轴上的x1=0、x2=6 处分别固定一点电荷,电量及电性已标在图上,图中虚线是两电荷连线的垂直平分线,虚线与连线交与O点.下列说法正确的是( )
如图所示,在x轴上的x1=0、x2=6 处分别固定一点电荷,电量及电性已标在图上,图中虚线是两电荷连线的垂直平分线,虚线与连线交与O点.下列说法正确的是( )| A. | 在x轴上O点的场强最强 | B. | 在虚线上各点电势相等 | ||
| C. | 场强为0 的点在x轴上x>6的某处 | D. | 在x轴上x<0的各点场强沿-x方向 |
 如图所示,真空中同一平面内MN直线上固定电荷量分别为-9Q和+Q的两个点电荷,两者相距为L,以+Q电荷为圆心,半径为$\frac{L}{2}$画圆,a、b、c、d是圆周上四点,其中a、b在MN直线上,c、d两点连线过+Q且垂直于直线MN,一电荷量为q的负试探电荷在圆周上运动,比较a、b、c、d四点,则下列说法正确的是( )
如图所示,真空中同一平面内MN直线上固定电荷量分别为-9Q和+Q的两个点电荷,两者相距为L,以+Q电荷为圆心,半径为$\frac{L}{2}$画圆,a、b、c、d是圆周上四点,其中a、b在MN直线上,c、d两点连线过+Q且垂直于直线MN,一电荷量为q的负试探电荷在圆周上运动,比较a、b、c、d四点,则下列说法正确的是( )| A. | b点电场强度最大 | B. | c、d两处的电场强度相等 | ||
| C. | 电荷q在b点的电势能最大 | D. | 电荷q在a点的电势能最大 |
 某同学研究碰撞问题,设计了如图所示的装置.天花板下用等长轻细线竖直悬挂两弹性小球,球大小可以忽略,细线长度为R,A球质量为m,B球质量为M,其中M=3m,重力加速度为g.现将A球拉至水平位置,保持细线伸直、无张力(如图虚线所示),给A球以竖直向下的初速度,使A、B两球在最低点发生弹性正碰,发现A球刚好能弹回初始的水平位置.求:
某同学研究碰撞问题,设计了如图所示的装置.天花板下用等长轻细线竖直悬挂两弹性小球,球大小可以忽略,细线长度为R,A球质量为m,B球质量为M,其中M=3m,重力加速度为g.现将A球拉至水平位置,保持细线伸直、无张力(如图虚线所示),给A球以竖直向下的初速度,使A、B两球在最低点发生弹性正碰,发现A球刚好能弹回初始的水平位置.求: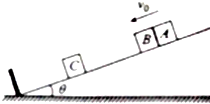 如图所示,倾角为θ=30°的斜面固定在水平面上,斜面底端有一挡板与之垂直,同种材料制成的可看为质点的小物块A、B、C,其质量分别为m、2m、2m,物块C静止在物块B与挡板之间某一位置.小物块A、B靠在一起,其间夹有少量炸药,一起以v0=4m/s的速度沿斜面匀速下滑,当A、B与挡板距离为L=1.75m时炸药爆炸,炸药爆炸后A的速度恰好变为零,随后小物块B沿斜面向下运动并与小物块C发生弹性碰撞,接着物块C与挡板也发生弹性碰撞.碰后物块C沿斜面上滑,最后物块B与A碰撞并粘成一体.取g=10m/s2,求物块B与A刚碰撞后的速度大小v共.
如图所示,倾角为θ=30°的斜面固定在水平面上,斜面底端有一挡板与之垂直,同种材料制成的可看为质点的小物块A、B、C,其质量分别为m、2m、2m,物块C静止在物块B与挡板之间某一位置.小物块A、B靠在一起,其间夹有少量炸药,一起以v0=4m/s的速度沿斜面匀速下滑,当A、B与挡板距离为L=1.75m时炸药爆炸,炸药爆炸后A的速度恰好变为零,随后小物块B沿斜面向下运动并与小物块C发生弹性碰撞,接着物块C与挡板也发生弹性碰撞.碰后物块C沿斜面上滑,最后物块B与A碰撞并粘成一体.取g=10m/s2,求物块B与A刚碰撞后的速度大小v共.