题目内容
7．
如图所示，物体沿足够长的斜面向上运动，经过 A 点时具有动能 120J，当它向上滑 行到 B 点时，动能减少了 90J，机械能损失了 30J，则物体回到 A 点时的动能为（ ）| A． | 100J | B． | 40J | C． | 20J | D． | 60J |
分析 物体上滑过程中受重力、支持力和滑动摩擦力，从A到B的过程，由动能定理和功能原理分别列式，得到重力做功和摩擦力做功的关系，再对上滑的整个过程研究，求出克服摩擦力做功，而下滑与上滑两个过程克服摩擦力做功相等，最后由功能关系求物体回到 A 点时的动能．
解答 解：物体上滑过程中受重力、支持力和摩擦力，从A到B的过程，根据动能定理，有：
-mg•lABsinθ-f•lAB=EKB-EKA=-90J
机械能减小量等于克服摩擦力做的功，故有：f•lAB=EB-EA=30J
联立解得 f=$\frac{1}{2}$mgsinθ．且知克服重力做功是克服摩擦力做功的2倍．
物体上滑的整个过程中，动能减少量为120J，克服重力做功与克服摩擦力做功之和是120J，可知，克服摩擦力做功为40J，机械能减少了40J，下滑的过程中，克服摩擦力做功也为40J，机械能又减少了40J，所以物体回到 A 点时的动能为120J-80J=40J．
故B正确，ACD错误
故选：B
点评 解决本题的关键是要掌握常见的功与能关系：合力的功（总功）等于动能增加量；重力做功等于重力势能的减小量；除重力外其余力做的功等于机械能的增加量．
练习册系列答案
阅读快车系列答案
相关题目
10．静止的实验火箭，总质量为M，当它以对地速度v0喷出质量为△m的高温气体后，火箭的速度为（ ）
| A． | $\frac{△m}{M-△m}$ v0 | B． | -$\frac{△m}{M-△m}$ v0 | C． | $\frac{△m}{M}$ v0 | D． | -$\frac{△m}{M}$ v0 |
18．
如图所示，光滑管道，A为距离地面高1m的起点，B为圆弧轨道和水平轨道连接点，C为弹簧原长端点，从A点由静止释放0.1kg的小球，最后静止时压缩弹簧至D点，那么（ ）
如图所示，光滑管道，A为距离地面高1m的起点，B为圆弧轨道和水平轨道连接点，C为弹簧原长端点，从A点由静止释放0.1kg的小球，最后静止时压缩弹簧至D点，那么（ ）| A． | 小球在A处动能为1J | |
| B． | 小球在B处的速度为20m/s | |
| C． | 当小球动能为0.5J时一定位于C、D之间 | |
| D． | 小球位于C、D之间时动能一定大于0而小于1J |
15．
如图所示，一根橡皮筋上端固定在O点，下端栓一个物块，开始时，物块处于静止且橡皮筋处于伸长状态，现对小球施加一个水平向右的外力F，使物块向右缓慢偏移，依次经过A点和B点，图中未标出具体位置，橡皮筋的伸长量始终处于弹性极限内，下列说法正确的是 （ ）
如图所示，一根橡皮筋上端固定在O点，下端栓一个物块，开始时，物块处于静止且橡皮筋处于伸长状态，现对小球施加一个水平向右的外力F，使物块向右缓慢偏移，依次经过A点和B点，图中未标出具体位置，橡皮筋的伸长量始终处于弹性极限内，下列说法正确的是 （ ）| A． | B点支持力比A点支持力大 | B． | 物块受到的摩擦力大小不变 | ||
| C． | 物块受到的摩擦力不断减小 | D． | 水平外力F不断增大 |
2．有关放射性知识，下列说法中正确的是（ ）
| A． | β衰变是原子核内的中子转化成质子和电子从而放出电子的过程 | |
| B． | γ射线一般伴随着α或β射线产生，这三种射线中，α粒子动能很大，因此贯穿物质的本领很强，γ射线电离能力最强 | |
| C． | 放射性的原子核发生衰变后产生的新核从高能级向低能级跃迁时，辐射出γ射线 | |
| D． | ${\;}_{7}^{15}$N+${\;}_{1}^{1}$H→${\;}_{6}^{12}$C+${\;}_{2}^{4}$He是α衰变方程 |
12．
如图所示，轻弹簧的一端与物块P相连，另一端固定在木板上．先将木板水平放置，并使弹簧处于拉伸状态．缓慢抬起木板的右端，使倾角逐渐增大，直至物块P刚要沿木板向下滑动，在这个过程中，关于物块P所受静摩擦力的大小和使物体紧压斜面的力，说法正确的是（ ）
如图所示，轻弹簧的一端与物块P相连，另一端固定在木板上．先将木板水平放置，并使弹簧处于拉伸状态．缓慢抬起木板的右端，使倾角逐渐增大，直至物块P刚要沿木板向下滑动，在这个过程中，关于物块P所受静摩擦力的大小和使物体紧压斜面的力，说法正确的是（ ）| A． | 一直增大，一直增大 | B． | 一直减小，一直增大 | ||
| C． | 先减小后增大，一直减小 | D． | 先增大后减小，一直减小 |
19．
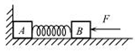如图所示，质量分别为m和2m的 A、B两个木块间用轻弹簧相连，放在光滑水平面上，A紧靠竖直墙．用水平力F将B向左压，使弹簧被压缩一定长度，静止后弹簧储存的弹性势能为 E．这时突然撤去 F，关于A、B和弹簧组成的系统，下列说法中正确的是（ ）
如图所示，质量分别为m和2m的 A、B两个木块间用轻弹簧相连，放在光滑水平面上，A紧靠竖直墙．用水平力F将B向左压，使弹簧被压缩一定长度，静止后弹簧储存的弹性势能为 E．这时突然撤去 F，关于A、B和弹簧组成的系统，下列说法中正确的是（ ）| A． | 撤去 F 后，系统动量守恒，机械能守恒 | |
| B． | 撤去 F 后，A 离开竖直墙前，系统动量不守恒，机械能守恒 | |
| C． | 撤去 F 后，A 离开竖直墙后，弹簧的弹性势能最大值为$\frac{E}{3}$ | |
| D． | 撤去 F 后，A 离开竖直墙后，弹簧的弹性势能最大值为 E |
16．
如图所示，三个小球的质量均为m，B、C两球用轻弹簧连接后放在光滑的水平面上，A球以速度v0沿B、C两球球心的连线向B球运动，碰后A、B两球粘在一起．对A、B、C及弹簧组成的系统，下列说法正确的是（ ）
如图所示，三个小球的质量均为m，B、C两球用轻弹簧连接后放在光滑的水平面上，A球以速度v0沿B、C两球球心的连线向B球运动，碰后A、B两球粘在一起．对A、B、C及弹簧组成的系统，下列说法正确的是（ ）| A． | 机械能守恒，动量守恒 | |
| B． | 机械能不守恒，动量守恒 | |
| C． | 三球速度相等时，弹簧恰好恢复原长 | |
| D． | 三球速度相等后，将一起做匀速运动 |
19．物块从斜面顶端由静止沿斜面下滑，斜面的倾角为θ=45°，物块与斜面间的动摩擦因数为μ，物块滑到斜面底端时速度大小为v，现将物块从斜面底端以一定的初速度沿斜面上滑，滑到斜面顶端时速度刚好为零，则初速度的大小为（ ）
| A． | $\sqrt{\frac{1+μ}{1-μ}}$v | B． | $\sqrt{\frac{1-μ}{1+μ}}$v | C． | $\sqrt{\frac{1+{μ}^{2}}{1-{μ}^{2}}}$v | D． | $\sqrt{\frac{1-{μ}^{2}}{1+{μ}^{2}}}$v |