题目内容
19.物块从斜面顶端由静止沿斜面下滑,斜面的倾角为θ=45°,物块与斜面间的动摩擦因数为μ,物块滑到斜面底端时速度大小为v,现将物块从斜面底端以一定的初速度沿斜面上滑,滑到斜面顶端时速度刚好为零,则初速度的大小为( )| A. | $\sqrt{\frac{1+μ}{1-μ}}$v | B. | $\sqrt{\frac{1-μ}{1+μ}}$v | C. | $\sqrt{\frac{1+{μ}^{2}}{1-{μ}^{2}}}$v | D. | $\sqrt{\frac{1-{μ}^{2}}{1+{μ}^{2}}}$v |
分析 物块在运动过程中重力与摩擦力做功,应用动能定理可以求出初速度大小.
解答 解:设斜面的长度为L,由动能定理得:
下滑过程:mgLsinθ-μmgLcosθ=$\frac{1}{2}$mv2-0,
上滑过程:-mgLsinθ-μmgLcosθ=0-$\frac{1}{2}$mv02,
解得:v0=$\sqrt{\frac{1+μ}{1-μ}}$v,故A正确,BCD错误;
故选:A.
点评 本题考查了求物块的初速度问题,分析清楚物块的运动过程与受力情况是解题的关键,应用动能定理即可解题;本题也可以应用牛顿第二定律与运动学公式求解.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
7. 如图所示,物体沿足够长的斜面向上运动,经过 A 点时具有动能 120J,当它向上滑 行到 B 点时,动能减少了 90J,机械能损失了 30J,则物体回到 A 点时的动能为( )
如图所示,物体沿足够长的斜面向上运动,经过 A 点时具有动能 120J,当它向上滑 行到 B 点时,动能减少了 90J,机械能损失了 30J,则物体回到 A 点时的动能为( )
 如图所示,物体沿足够长的斜面向上运动,经过 A 点时具有动能 120J,当它向上滑 行到 B 点时,动能减少了 90J,机械能损失了 30J,则物体回到 A 点时的动能为( )
如图所示,物体沿足够长的斜面向上运动,经过 A 点时具有动能 120J,当它向上滑 行到 B 点时,动能减少了 90J,机械能损失了 30J,则物体回到 A 点时的动能为( )| A. | 100J | B. | 40J | C. | 20J | D. | 60J |
8. 如图所示,质量为M的带有$\frac{1}{4}$光滑圆弧形轨道的小车静止置于光滑的水平面上,现有一质量也为M的小球以速度v0水平冲上小车,到达某一高度后,小球又返回到小车的最左端,则下列说法中正确的是( )
如图所示,质量为M的带有$\frac{1}{4}$光滑圆弧形轨道的小车静止置于光滑的水平面上,现有一质量也为M的小球以速度v0水平冲上小车,到达某一高度后,小球又返回到小车的最左端,则下列说法中正确的是( )
 如图所示,质量为M的带有$\frac{1}{4}$光滑圆弧形轨道的小车静止置于光滑的水平面上,现有一质量也为M的小球以速度v0水平冲上小车,到达某一高度后,小球又返回到小车的最左端,则下列说法中正确的是( )
如图所示,质量为M的带有$\frac{1}{4}$光滑圆弧形轨道的小车静止置于光滑的水平面上,现有一质量也为M的小球以速度v0水平冲上小车,到达某一高度后,小球又返回到小车的最左端,则下列说法中正确的是( )| A. | 在此过程中,小球和小车组成的系统动量守恒 | |
| B. | 此小球将做自由落体运动 | |
| C. | 在此过程中,小球对小车做的功为$\frac{1}{2}$Mv02 | |
| D. | 小球在$\frac{1}{4}$弧形槽上上升的最大高度为$\frac{{{v}_{0}}^{2}}{2g}$ |
1.下列说法正确的是( )
| A. | β衰变现象说明原子核外存在电子 | |
| B. | 温度升高,放射性元素的半哀期变小 | |
| C. | 氢原子从基态向较高能量态跃迁时,电子的动能减小 | |
| D. | α粒子散射实验表明核外电子轨道是量子化的 |
 如图所示,一定质量的理想气体从状态A变化到状态B,再由状态B变化到状态C,已知状态A的温度为300K,则由状态A变化到状态B的过程中,气体的内能增大(填“增大”、“减小”或“不变”);B、C两状态气体的内能分别为UB和UC,则UB等于UC(填“大于”、“等于”或“小于”).
如图所示,一定质量的理想气体从状态A变化到状态B,再由状态B变化到状态C,已知状态A的温度为300K,则由状态A变化到状态B的过程中,气体的内能增大(填“增大”、“减小”或“不变”);B、C两状态气体的内能分别为UB和UC,则UB等于UC(填“大于”、“等于”或“小于”). 质量为m的小球由高为H与水平夹角为为α的光滑斜面顶端无初速滑到底端过程中,重力、弹力、合力的冲量各是多大?
质量为m的小球由高为H与水平夹角为为α的光滑斜面顶端无初速滑到底端过程中,重力、弹力、合力的冲量各是多大?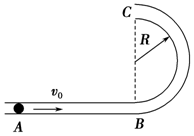 如图所示,用细圆管组成的光滑轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,圆管截面半径r?R.有一质量为m,半径比r略小的光滑小球以水平初速度v0射入圆管.
如图所示,用细圆管组成的光滑轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,圆管截面半径r?R.有一质量为m,半径比r略小的光滑小球以水平初速度v0射入圆管.