题目内容
16.在水平恒力作用下,若将一个质量为m的小球由静止释放,运动中小球的速度与竖直方向夹角为37°,现将该小球以初速度v0竖直向上抛出.求运动过程中(1)小球受到的水平恒力的大小;
(2)经过多少时间小球速度最小;最小速度的大小及方向.
分析 (1)小球静止释放时,沿着合力的方向运动,由于小球所受的水平力与重力均为恒力,故其运动方向和合外力方向一致,根据平行四边形定则可以求出水平恒力的大小;
(2)将该小球以初速度v0竖直向上抛出后,水平方向做匀加速直线运动,竖直方向上做竖直上抛运动,小球的运动类似于斜上抛运动,当速度与合力垂直时,速度最小,先根据速度关系求出时间,再由速度公式求出分速度,最后求解最小的速度.
解答  解:(1)根据题设条件可知,小球静止释放时,合外力和竖直方向夹角应为37°,如图.
解:(1)根据题设条件可知,小球静止释放时,合外力和竖直方向夹角应为37°,如图.
所以水平恒力大小为:F=mgtan37°=$\frac{3}{4}$mg
(2)将该小球以初速度v0竖直向上抛出后,水平方向做初速度为零的匀加速直线运动,竖直方向上做竖直上抛运动.
水平方向的分加速度为:ax=$\frac{F}{m}$=$\frac{3}{4}$g
小球的运动类似于斜上抛运动,当速度与合力垂直时,速度最小,如图.此时速度与水平方向的夹角为37°.
设从抛出到速度最小的时间为t.则有:
tan37°=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{{v}_{0}-gt}{\frac{3}{4}gt}$
解得:t=$\frac{16{v}_{0}}{25g}$
则有:vx=at=$\frac{12}{25}$v0,vy=v0-gt=$\frac{9}{25}$v0
最小的速度为:vmin=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=$\frac{3}{5}$v0
答:(1)小球受到的水平恒力的大小是$\frac{3}{4}$mg.
(2)经过$\frac{16{v}_{0}}{25g}$时间小球速度最小;最小速度的大小是$\frac{3}{5}$v0,方向与水平方向成37°斜向上.
点评 本题中物体在复合场中运动,运用运动的分解法研究物体运动,可与斜上抛运动类比来理解.要正确进行受力分析,弄清运动形式,利用相应物理规律求解.对于最小速度,也可以列出速度与时间的关系式,运用数学知识求解.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 如图所示,光滑轨道LMNPQMK固定在水平地面上,轨道平面在竖直面内,MNPQM是半径为R的圆形轨道,轨道LM与圆形轨道MNPQM在M点相切,轨道MK与圆形轨道MNPQM在M点相切,b点、P点在同一水平面上,K点位置比P点低,b点离地高度为2R,a点离地高度为2.5R.若将一个质量为m的小球从左侧轨道上不同位置由静止释放,关于小球的运动情况,以下说法中正确的是( )
如图所示,光滑轨道LMNPQMK固定在水平地面上,轨道平面在竖直面内,MNPQM是半径为R的圆形轨道,轨道LM与圆形轨道MNPQM在M点相切,轨道MK与圆形轨道MNPQM在M点相切,b点、P点在同一水平面上,K点位置比P点低,b点离地高度为2R,a点离地高度为2.5R.若将一个质量为m的小球从左侧轨道上不同位置由静止释放,关于小球的运动情况,以下说法中正确的是( )| A. | 若将小球从LM轨道上a点由静止释放,小球一定不能沿轨道运动到K点 | |
| B. | 若将小球从LM轨道上b点由静止释放,小球一定能沿轨道运动到K点 | |
| C. | 若将小球从LM轨道上a、b点之间任一位置由静止释放,小球一定能沿轨道运动到K点 | |
| D. | 若将小球从LM轨道上a点以上任一位置由静止释放,小球沿轨道运动到K点后做斜上抛运动,小球做斜上抛运动时距离地面的最大高度一定小于由静止释放时的高度 |
 伽利略的理想斜面实验反映了一个重要事实:如果忽略空气阻力和摩擦力,让小球从左边斜面上某一点滚下,必将冲上右边斜面的相同高度处,这说明:小球在运动过程中有一个物理量是不变的,这个物理量是( )
伽利略的理想斜面实验反映了一个重要事实:如果忽略空气阻力和摩擦力,让小球从左边斜面上某一点滚下,必将冲上右边斜面的相同高度处,这说明:小球在运动过程中有一个物理量是不变的,这个物理量是( )| A. | 机械能 | B. | 速度 | C. | 加速度 | D. | 弹力 |
| A. | 若v0>$\sqrt{gH}$,两物体相遇时,B正在下降途中 | |
| B. | 若v0=$\sqrt{gH}$,两物体在地面相遇 | |
| C. | 若$\sqrt{gH}$>v0>$\sqrt{\frac{gH}{2}}$,两物体相遇时B物体正在空中下落 | |
| D. | 若v0=$\sqrt{\frac{gH}{2}}$,则两物体在地面相遇 |
| A. | 1000 J | B. | 2000 J | C. | 3000 J | D. | 4000 J |
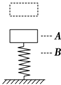 一物块从某一高度自由落下,落在竖立于地面的轻弹簧上.物块在A处开始与弹簧接触,到B处时物块速度为零,然后被弹回.下列说法正确的是( )
一物块从某一高度自由落下,落在竖立于地面的轻弹簧上.物块在A处开始与弹簧接触,到B处时物块速度为零,然后被弹回.下列说法正确的是( )| A. | 物块从A处下降到B处的过程中,速率不断减小 | |
| B. | 物块从B处上升到A处的过程中,速率不断增大 | |
| C. | 物块在B处时,所受合力为零 | |
| D. | 物块从A处下降到B处的过程中速率先增大,后减小 |
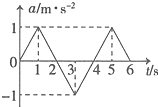 一质点以v0=5m/s的初速度从t=0时刻开始做直线运动,其加速度随时t变化的图
一质点以v0=5m/s的初速度从t=0时刻开始做直线运动,其加速度随时t变化的图象如图所示,则下列说法正确的是( )
| A. | 第1s末质点的速度为6m/s | B. | 运动过程中质点的最大速度为6m/s | ||
| C. | 第ls内质点的位移为5.25m | D. | 4s末质点回到t=0时刻的位置 |
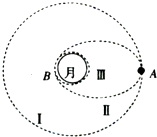 探月工程二期“嫦娥三号”成功发射.这极大地提高了同学们对月球的关注程度,以下是某同学就有关月球的知识设计的问题情景:
探月工程二期“嫦娥三号”成功发射.这极大地提高了同学们对月球的关注程度,以下是某同学就有关月球的知识设计的问题情景: