题目内容
12. 探月工程二期“嫦娥三号”成功发射.这极大地提高了同学们对月球的关注程度,以下是某同学就有关月球的知识设计的问题情景:
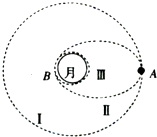
探月工程二期“嫦娥三号”成功发射.这极大地提高了同学们对月球的关注程度,以下是某同学就有关月球的知识设计的问题情景:假设月球半径为R,“嫦娥三号”在离月球中心距离为r的圆形轨道I运动,其运动周期为T,到达轨道的A点点火变轨进入椭圆轨道II,到达轨道的近月B再次点火变轨到贴近月球表面的轨道III绕月球作圆周运动,此时“嫦娥三号”的速度即为该星球的第一宇宙速度.在轨道III运行多圈后,“嫦娥三号”点火减速实现在月球上的软着陆.
(1)月球表面的重力加速度;
(2)月球的第一宇宙速度.
分析 (1)嫦娥三号绕圆形轨道I做匀速圆周运动时,万有引力提供向心力G$\frac{Mm}{{r}^{2}}$=mr($\frac{2π}{T}$)2,又因为在月球表面万有引力近似等于重力G$\frac{Mm}{{R}^{2}}$=mg,联立可解得月球表面的重力加速度g.
(2)由万有引力提供向心力得:G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,结合G$\frac{Mm}{{R}^{2}}$=mg,代入g的值,可解得月球的第一宇宙速度
解答 解:(1)设月球的质量为M,嫦娥三号的质量为m.嫦娥三号绕圆形轨道I做匀速圆周运动时,由万有引力提供向心力得:G$\frac{Mm}{{r}^{2}}$=mr($\frac{2π}{T}$)2,
设月球表面的重力加速度为g,在月球表面万有引力近似等于重力:G$\frac{Mm}{{R}^{2}}$=mg,
联立解得:g=$\frac{4{π}^{2}{r}^{3}}{{T}^{2}{R}^{2}}$
(2)嫦娥三号在贴近月球表面的圆轨道上运动的线速度为v,由万有引力提供向心力得:G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,
联立以上各式,解得:v=$\frac{2πr}{T}\sqrt{\frac{r}{R}}$
答:(1)月球表面的重力加速度为$\frac{4{π}^{2}{r}^{3}}{{T}^{2}{R}^{2}}$
(2)月球的第一宇宙速度为$\frac{2πr}{T}\sqrt{\frac{r}{R}}$
点评 本题主要考查万有提供向心力G$\frac{Mm}{{r}^{2}}$=mr($\frac{2π}{T}$)2)2和在星球表面万有引力近似等于重力G$\frac{Mm}{{r}^{2}}$=mg,这两个关系对于解决天体运动问题非常重要,一定要理解并掌握.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | 速度不变 | B. | 动能不变 | C. | 加速度不变 | D. | 受力不变 |
| A. | 弹簧秤 | B. | 秒表 | C. | 重垂线 | D. | 天平 |
| A. | 该行星的半径为$\frac{vT}{2π}$ | B. | 该行星的平均密度为$\frac{3π}{{G{T^2}}}$ | ||
| C. | 该行星的质量为$\frac{{4{π^2}v}}{{G{T^2}}}$ | D. | 该行星表面的重力加速度为$\frac{2πv}{T}$ |
 动摩擦因数为μ2,木块与木板间的动摩擦因数为μ1,重力加速度为g,且M=m,μ1=3μ,μ2=μ.求:
动摩擦因数为μ2,木块与木板间的动摩擦因数为μ1,重力加速度为g,且M=m,μ1=3μ,μ2=μ.求: 已知一质量为m的物块在力F的作用下,由静止开始在粗糙水平面上向右运动,当运动到距离出发点x位移时,改变力F的方向,大小不变,直至回到原出发点,设动摩擦因数为μ.求:
已知一质量为m的物块在力F的作用下,由静止开始在粗糙水平面上向右运动,当运动到距离出发点x位移时,改变力F的方向,大小不变,直至回到原出发点,设动摩擦因数为μ.求: 如图所示为某汽车作直线运动的v-t图象,从图象可知,汽车在前10s的加速度大小是0.5 m/s2,在前40s内通过的位移等于150m.
如图所示为某汽车作直线运动的v-t图象,从图象可知,汽车在前10s的加速度大小是0.5 m/s2,在前40s内通过的位移等于150m. 物体A与B重叠放置于光滑水平面上,如图所示,已知物体A的质量mA为5kg,物体B的质量mB为3kg.大小为12N的水平力F作用在物体A上,使AB二物体(保持相对静止)一起沿力F的方向,做匀加速直线运动.求运动过程中,B物体受到A物体对它的摩擦力?
物体A与B重叠放置于光滑水平面上,如图所示,已知物体A的质量mA为5kg,物体B的质量mB为3kg.大小为12N的水平力F作用在物体A上,使AB二物体(保持相对静止)一起沿力F的方向,做匀加速直线运动.求运动过程中,B物体受到A物体对它的摩擦力?