题目内容
19. 如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠B=60°,AB边长为L.一束与BC面成θ=30°角的光从BC面中点射入三棱镜,进入三棱镜后折射光线从AB边平行AC边射出.不考虑光线在AB边上的反射情况.已知光在真空中速度为C.求:
如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠B=60°,AB边长为L.一束与BC面成θ=30°角的光从BC面中点射入三棱镜,进入三棱镜后折射光线从AB边平行AC边射出.不考虑光线在AB边上的反射情况.已知光在真空中速度为C.求:(1)三棱镜的折射率;
(2)光通过三棱镜的时间.
分析 (1)作出光路图,由几何关系求出光线射到AB面上时的入射角和折射角,再求出三棱镜的折射率.
(2)由几何知识求光线在棱镜中传播的路程,由v=$\frac{c}{n}$求出光在棱镜中传播的速度,即可求解传播时间.
解答  解:(1)作出光路图,由几何关系可知,光线在AB边上的入射角 i=60°,折射角 γ=30°
解:(1)作出光路图,由几何关系可知,光线在AB边上的入射角 i=60°,折射角 γ=30°
根据折射定律得:n=$\frac{sini}{sinγ}$
解得三棱镜的折射率为:n=$\sqrt{3}$
(2)光在棱镜中的传播速度为:v=$\frac{c}{n}$
由几何关系可知:MN=$\frac{L}{2}$,NQ=$\frac{L}{4}$
则光在棱镜中通过的总路程为:s=MN+NQ=$\frac{3}{4}$L
光通过三棱镜的时间为:t=$\frac{s}{v}$
解得:t=$\frac{3\sqrt{3}L}{4c}$
答:(1)三棱镜的折射率是$\sqrt{3}$;
(2)光通过三棱镜的时间是$\frac{3\sqrt{3}L}{4c}$.
点评 解决本题的关键是画出光路图,运用折射定律和几何关系进行求解.

练习册系列答案
相关题目
7.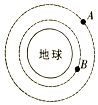 如图所示,两质量相等的卫星A、B绕地球做匀速圆周运动,用R、T、Ek、S分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的是( )
如图所示,两质量相等的卫星A、B绕地球做匀速圆周运动,用R、T、Ek、S分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的是( )
 如图所示,两质量相等的卫星A、B绕地球做匀速圆周运动,用R、T、Ek、S分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的是( )
如图所示,两质量相等的卫星A、B绕地球做匀速圆周运动,用R、T、Ek、S分别表示卫星的轨道半径、周期、动能、与地心连线在单位时间内扫过的面积.下列关系式正确的是( )| A. | TA<TB | B. | EkA>EkB | ||
| C. | SA=SB | D. | $\frac{{R}_{A}^{3}}{{T}_{A}^{2}}$=$\frac{{R}_{B}^{3}}{{T}_{B}^{2}}$ |
14.关于物理学家做出的贡献,下列说法正确的是( )
| A. | 奥斯特发现了电磁感应现象 | |
| B. | 韦伯发现了电流的磁效应,揭示了电现象和磁现象之间的联系 | |
| C. | 洛伦兹发现了磁场对电流的作用规律 | |
| D. | 安培观察到通电螺旋管和条形磁铁的磁场很相似,提出了分子电流假说 |
1.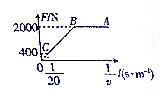 在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )
在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )
 在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )
在检测某款电动车性能的实验中,一质量为8×102kg的电动车由静止开始沿平直公路行驶,经30s达到最大行驶速度20m/s.此过程中,利用传感器测得不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象如图所示,其中AB、AC均为直线.已知电动车行驶中所受的阻力恒定,取g=10m/s2.下列说法正确的是( )| A. | 在AB过程中,电动车做匀加速运动 | |
| B. | 在整个过程中,电动车受到的阻力为2000N | |
| C. | 在整个过程中,电动车发动机的最大功率为8000W | |
| D. | 在整个过程中,电动车克服阻力做的功为72000J |
18.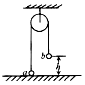 如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
 如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )
如图所示,一根足够长的、不可伸长的柔软轻绳跨过光滑定滑轮(定滑轮质量不计),绳两端各系一小球a和b,a球质量为m,b球质量为M(M>m),用手托住b球,b高度为h,此时轻绳刚好拉紧,从静止开始释放b,a能上升的最大高度为(a球不会与滑轮碰撞)( )| A. | $\frac{m}{M+m}$h | B. | $\frac{M}{M+m}$h | C. | $\frac{2m}{M+m}$h | D. | $\frac{2M}{M+m}$h |
 第24届冬季奥林匹克运动会--北京-张家口冬季奥运会,将在2022年2月4日至2月20日在北京市和张家口市联合举行.这是中国历史上第一次举办冬季奥运会.如图所示,质量m=60kg的运动员从长直助滑道AB的A处由静止开始滑下.为了改变运动员的运动方向,在助滑道与起跳台之间用一段弯曲滑道衔接,其中最低点C处附近是一段以O为圆心的圆弧.圆弧半径R=12.5m.已知运动员在A、C间运动时阻力做功W=-13050J.A与C的竖直高度差H=53m,重力加速度g=10m/s2.求:
第24届冬季奥林匹克运动会--北京-张家口冬季奥运会,将在2022年2月4日至2月20日在北京市和张家口市联合举行.这是中国历史上第一次举办冬季奥运会.如图所示,质量m=60kg的运动员从长直助滑道AB的A处由静止开始滑下.为了改变运动员的运动方向,在助滑道与起跳台之间用一段弯曲滑道衔接,其中最低点C处附近是一段以O为圆心的圆弧.圆弧半径R=12.5m.已知运动员在A、C间运动时阻力做功W=-13050J.A与C的竖直高度差H=53m,重力加速度g=10m/s2.求:
 如图,设想光滑水平面上有两同样大小的小球,质量为m1的小球A以v1速度向右作匀速直线运动,与质量为m2的静止小球B发生碰撞,碰后小球A速度变为v1′,小球B速度变为v2′,方向均向右,若规定向右为正方向.试分析:
如图,设想光滑水平面上有两同样大小的小球,质量为m1的小球A以v1速度向右作匀速直线运动,与质量为m2的静止小球B发生碰撞,碰后小球A速度变为v1′,小球B速度变为v2′,方向均向右,若规定向右为正方向.试分析: