题目内容
7.如今,合肥一中的每间教室里都有饮水机,纯净水的质量关乎每一名学生的身体健康.纯净水质量是否合格的一项重要指标是它的电导率λ是否超标(电导率λ即为电阻率ρ的倒数).(1)某同学选用一根粗细均匀且绝缘性能良好的圆柱形塑料直管装满纯净水样品(直管两端用薄金属圆片电极密封)来测定样品的电导率(不考虑温度对电阻的影响):实验中,该同学分别用刻度尺和游标为20分度的游标卡尺测定塑料管的长度和内径,刻度尺和游标卡尺的示数分别如图甲、乙所示,则可读出塑料管的长度L=10.50cm、内径d=11.30mm.
(2)该同学用下列器材测定样品的电阻:

a.电压表V(量程0~3V,内阻约为5kΩ;量程0~15V,内阻约为25kΩ);
b.电流表A(量程0~10mA,内阻约为2Ω;量程0~50mA,内阻约为0.4Ω);
c.滑动变阻器R(0~20Ω,2A);
d.学生电源E(电动势4.5V,内阻很小);
c.开关S及导线若干.
该同学先用多用电表粗测管内水样品的电阻值约为500Ω,要求用尽量精确的方法测出其电阻值,请在图丙中连接实验电路图(图中有六根导线已经接好).
(3)在不损坏电表的前提下,将滑动变阻器滑片P从最左端向右滑动,随滑片P移动距离x的增加,被测水样品两端的电压U也随之增加,则在图丁反映U-x关系的示意图中正确的是图线d(填“a”“b”“c”或“d”).

分析 (1)由图示刻度尺确定其分度值,然后读出其示数;游标卡尺读数的方法是主尺读数加上游标读数,不需估读;
(2)合理选择实验器材,先选必要器材,再根据要求满足安全性,准确性,方便操作的原则选择待选器材.电流表的接法要求大电阻内接法,小电阻外接法.滑动变阻器是小电阻控制大电阻,用分压式接法.根据电路图来连接实物图,注意电表的正负极,并分几个回路来连接;
(3)根据闭合电路欧姆定律,结合电阻定律,即可求解.
解答  解:(1)刻度尺读数:0.2050-0.1000=0.1050m;
解:(1)刻度尺读数:0.2050-0.1000=0.1050m;
游标卡尺的主尺读数为11mm,游标读数为0.05×6mm=0.30mm,所以最终读数为11.30mm;
(2)因电源的电压为4.5V,因此电压表选择3V量程;由于阻值约为500Ω的电阻Rx的,
根据欧姆定律可知,电流的最大值为9mA,从精确角来说,所以电流表选择量程0~10mA;
根据待测电阻的阻值与电压表及电流表的阻值,可知,待测电阻的阻值偏大,因此选择电流表内接法,
根据电路图来连接实物图原则,注意电表的正负极,并分几个回路来连接.如图所示;
(3)根据闭合电路欧姆定律与电阻定律,U=IRX=$\frac{E}{ρ\frac{L-x}{S}+{R}_{x}}{R}_{x}$,
当滑片P移动距离x的增加,被测电阻Rx两端的电压增大,
但不成正比,且增加越来越快,则U-x图象如图d所示;
故答案为:(1)10.50,11.30;(2)如图所示;(3)d.
点评 解决本题的关键掌握游标卡尺读数的方法,主尺读数加上游标读数,不需估读;
同时还考查了同学们设计电路的能力,要弄清楚是内接法还是外接法,是分压还是限流法;
考查如何选择仪器,掌握选择的方法与原则;学会由电路图去连接实物图,注意电表的正负极;理解欧姆定律与电阻定律的应用,掌握误差的分析及其产生原因.

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案 如图是滑雪场的一条雪道.质量为70kg的某滑雪运动员由A点沿圆弧轨道滑下,在B点以5$\sqrt{3}$m/s的速度水平飞出,落到了倾斜轨道上的C点(图中未画出).不计空气阻力,θ=30°,g=10m/s2,则下列判断正确的是( )
如图是滑雪场的一条雪道.质量为70kg的某滑雪运动员由A点沿圆弧轨道滑下,在B点以5$\sqrt{3}$m/s的速度水平飞出,落到了倾斜轨道上的C点(图中未画出).不计空气阻力,θ=30°,g=10m/s2,则下列判断正确的是( )| A. | 该滑雪运动员腾空的时间为1s | |
| B. | BC两点间的落差为5$\sqrt{3}$m | |
| C. | 落到C点时重力的瞬时功率为3500$\sqrt{7}$W | |
| D. | 若该滑雪运动员从更高处滑下,落到C点时速度与竖直方向的夹角变小 |
 如图所示,一质量为m的金属杆可以无摩擦地沿水平的平行导轨滑行,两轨间宽为L,导轨与电阻R连接,放在竖直向的匀强磁场中,磁场的磁感应强度为B,杆的初速度为v,其余电阻不计,则( )
如图所示,一质量为m的金属杆可以无摩擦地沿水平的平行导轨滑行,两轨间宽为L,导轨与电阻R连接,放在竖直向的匀强磁场中,磁场的磁感应强度为B,杆的初速度为v,其余电阻不计,则( )| A. | 由于金属杆和导轨之间无摩擦力,回路中的感应电动势始终是BLv | |
| B. | 金属杆所受的安培力方向与初速度方向相反 | |
| C. | 金属杆所受的安培力逐渐增大 | |
| D. | 电阻R上产生的总焦耳热为$\frac{1}{2}$mv2 |
 如图所示,竖直固定放置的粗糙斜面AB的下端与光滑的圆弧轨道BCD的B端相切,圆弧轨道的半径为R,圆心O与A、D在同一水平面上,∠COB=θ=45°,现使一质量为m的小物体从D点无初速滑下,小物块与粗糙斜面AB间的动摩擦因数为μ<tanθ,则关于小物块的运动情况,下列说法正确的是( )
如图所示,竖直固定放置的粗糙斜面AB的下端与光滑的圆弧轨道BCD的B端相切,圆弧轨道的半径为R,圆心O与A、D在同一水平面上,∠COB=θ=45°,现使一质量为m的小物体从D点无初速滑下,小物块与粗糙斜面AB间的动摩擦因数为μ<tanθ,则关于小物块的运动情况,下列说法正确的是( )| A. | 小物块可能运动到A点 | |
| B. | 小物块最终将停在C点 | |
| C. | 小物块通过圆弧轨道最低点C时,对C点的最大压力为3mg | |
| D. | 小物块通过圆弧轨道最低点C时,对C点的最大压力为(3-$\sqrt{2}$μ)mg |
 如图所示,水平传送带以速度v匀速传动,一质量为m的小物块A由静止轻放在传送带上,若小物块与传送带间的动摩擦因数为μ,已知物块在传送带上先加速后匀速,下列说法中正确的是( )
如图所示,水平传送带以速度v匀速传动,一质量为m的小物块A由静止轻放在传送带上,若小物块与传送带间的动摩擦因数为μ,已知物块在传送带上先加速后匀速,下列说法中正确的是( )| A. | 摩擦力对物块一直做正功 | |
| B. | 摩擦力对传送带先做正功后不做功 | |
| C. | 系统转化为内能的能量为$\frac{1}{2}$mv2 | |
| D. | 物块加速阶段,传送带克服摩擦力做功的功率总为μmgv |
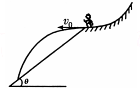 如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )
如图所示,在高台滑雪比赛中,某运动员从平台上以v0的初速度沿水平方向飞出后,落到倾角为θ的雪坡上(雪坡足够长).若运动员可视为质点,不计空气阻力,重力加速度为g,则( )| A. | 如果v0不同,运动员落到雪坡时的位置不同,速度方向也不同 | |
| B. | 如果v0不同,运动员落到雪坡时的位置不同,但空中运动时间相同 | |
| C. | 运动员刚要落到雪坡上时的速度大小为$\frac{{v}_{0}}{cosθ}$ | |
| D. | 运动员在空中经历的时间为$\frac{2{v}_{0}tanθ}{g}$ |
 如图所示,一块足够大的光滑平板能绕水平固定轴MN调节其与水平面所成的倾角.板上一根长为L=0.50m的轻细绳,它的一端系住一质量为m的小球,另一端固定在板上的O点.当平板的倾角固定为α时,先将轻绳平行于水平轴MN拉直,然后给小球一沿着平板并与轻绳垂直的初速度v0=3.0m/s.若小球能保持在板面内作圆周运动,求倾角α的最大值?(取重力加速度g=10m/s2,cos53°=0.6)
如图所示,一块足够大的光滑平板能绕水平固定轴MN调节其与水平面所成的倾角.板上一根长为L=0.50m的轻细绳,它的一端系住一质量为m的小球,另一端固定在板上的O点.当平板的倾角固定为α时,先将轻绳平行于水平轴MN拉直,然后给小球一沿着平板并与轻绳垂直的初速度v0=3.0m/s.若小球能保持在板面内作圆周运动,求倾角α的最大值?(取重力加速度g=10m/s2,cos53°=0.6) 如图为固定在竖直平面内的轨道,直轨道AB与光滑圆弧轨道BC相切,圆弧轨道的圆心角为37°,半径为r=0.25m,C端水平,AB段的动摩擦因数为0.5.竖直墙壁CD高H=0.2m,紧靠墙壁在地面上固定一个和CD等高,底边长L=0.3m的斜面.一个质量m=0.1kg的小物块(视为质点)在倾斜轨道上从距离B点l=0.5m处由静止释放,从C点水平抛出.重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图为固定在竖直平面内的轨道,直轨道AB与光滑圆弧轨道BC相切,圆弧轨道的圆心角为37°,半径为r=0.25m,C端水平,AB段的动摩擦因数为0.5.竖直墙壁CD高H=0.2m,紧靠墙壁在地面上固定一个和CD等高,底边长L=0.3m的斜面.一个质量m=0.1kg的小物块(视为质点)在倾斜轨道上从距离B点l=0.5m处由静止释放,从C点水平抛出.重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求: 某同学在测量一根弹簧的劲度系数实验中,得到的实验数据,作出图象如图所示,该弹簧的劲度系数k=54N/m(结果保留两位有效数字).
某同学在测量一根弹簧的劲度系数实验中,得到的实验数据,作出图象如图所示,该弹簧的劲度系数k=54N/m(结果保留两位有效数字).