题目内容
4. 如图所示,光滑绝缘的半圆形轨道固定于竖直平面内,半圆形轨道与光滑绝缘的水平地面相切于半圆的端点A.一质量为1kg的小球在水平地面上匀速运动,速度为v=6m/s,经A运动到轨道最高点B,最后又落在水平地面上的D点(图中未画出).已知整个空间存在竖直向下的匀强电场,小球带正电荷,小球所受电场力的大小等于2mg,g为重力加速度.
如图所示,光滑绝缘的半圆形轨道固定于竖直平面内,半圆形轨道与光滑绝缘的水平地面相切于半圆的端点A.一质量为1kg的小球在水平地面上匀速运动,速度为v=6m/s,经A运动到轨道最高点B,最后又落在水平地面上的D点(图中未画出).已知整个空间存在竖直向下的匀强电场,小球带正电荷,小球所受电场力的大小等于2mg,g为重力加速度.(1)当轨道半径R=0.1m时,求小球到达半圆形轨道B点时对轨道的压力;
(2)为使小球能运动到轨道最高点B,求轨道半径的最大值;
(3)轨道半径多大时,小球在水平地面上的落点D到A点距离最大,且最大距离为多少?
分析 (1)先由动能定理求出小球到达B点时的速度大小,再由牛顿第二定律求出轨道对小球的弹力,即可由牛顿第三定律得到小球对轨道的压力.
(2)当小球对轨道的压力恰好为零时,求出轨道半径的最大值Rm;
(3)小球离开B点后做平抛运动,根据高度求出平抛运动的时间,再根据初速度和时间求出平抛运动的水平位移表达式,与第1题中小球经过B点的速度联立,运用数学知识求解.
解答 解:(1)设小球到达圆轨道B点时速度为v,从A到B的过程中重力和电场力做功,由动能定理有:
-2mgR-2mg•2R=$\frac{1}{2}m{v}_{B}^{2}$-$\frac{1}{2}m{v}^{2}$
所以:${v}_{B}=\sqrt{{v}^{2}-12gR}$
据牛顿第二定律有:FN+mg+2mg=m$\frac{{v}_{B}^{2}}{R}$
代入数据解得:FN=210N
牛顿第三定律可知,小球到达圆轨道B点时对轨道的压力为:FN′=FN=210N,方向竖直向上.
(2)轨道半径越大,小球到达最高点的速度越小,当小球恰好到达最高点时,轨道对小球的作用力为零,则小球对轨道的压力也为零,此时轨道半径最大,则:
$\frac{m{v}_{min}^{2}}{R′}=mg+2mg$
又:-2mgR′-2mg•2R′=$\frac{1}{2}m{v}_{min}^{2}-\frac{1}{2}m{v}^{2}$,
代入数据解得轨道半径的最大值:R′=0.24m
(3)设小球类平抛运动的时间为t,在竖直方向上小球的加速度:a=$\frac{mg+2mg}{m}=3g$
所以有:2R″=$\frac{1}{2}•3g•{t}^{2}$
得:t=2$\sqrt{\frac{R″}{3g}}$
水平位移为:x=vBt=$\sqrt{{v}^{2}-12gR″}$•2$\sqrt{\frac{R″}{3g}}$=$2\sqrt{\frac{R″}{3g}({v}^{2}-12gR″)}$
当$\frac{R″}{3g}={v}^{2}-12gR″$时,水平位移x最大.
得:R″=0.2999m>R′
结合(2)的解答可知,当圆的半径为0.24m时,D到A的距离最大,
代入数据求得D到A最大距离为:xmax=0.48m,
答:(1)当轨道半径R=0.1m时,小球到达半圆形轨道B点时对轨道的压力是210N;
(2)为使小球能运动到轨道最高点B,轨道半径的最大值是0.24m;
(3)轨道半径是0.24m大时,小球在水平地面上的落点D到A点距离最大,且最大距离为0.48m.
点评 本题综合运用了动能定理、牛顿第二定律、平抛运动,综合性较强,关键理清过程,选择适当的定理或定律进行解题.

| A. | 三个离子离开偏转电场时的速度方向相同 | |
| B. | 三个离子在偏转电场中的位移相等 | |
| C. | 一价的氢离子、一价的氦离子离开电场时的动能相等 | |
| D. | 三个离子同时离开偏转电场 |
 如图所示,在方向竖直向下的匀强电场中,一绝缘轻细线一端固定于O点,另一端系一带正电的小球在竖直平面内做圆周运动.小球的电荷量为q,质量为m,绝缘细线长为L,电场的场强为E.若带电小球恰好能通过最高点A,则( )
如图所示,在方向竖直向下的匀强电场中,一绝缘轻细线一端固定于O点,另一端系一带正电的小球在竖直平面内做圆周运动.小球的电荷量为q,质量为m,绝缘细线长为L,电场的场强为E.若带电小球恰好能通过最高点A,则( )| A. | 在A点时小球的速度v1=$\sqrt{(\frac{qE}{m}-g)L}$ | |
| B. | 在A点时小球的速度v1=$\sqrt{(\frac{qE}{m}+g)L}$ | |
| C. | 运动到B点时细线对小球的拉力为6(mg+qE) | |
| D. | 小球运动到最低点B时的速度v2=$\sqrt{5(\frac{qE}{m}+g)L}$ |
| A. | 8Ek | B. | 4.25Ek | C. | 5Ek | D. | 4Ek |
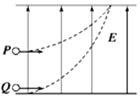 如图所示,质量相同的两个带电粒子P、Q以相同的初速度沿垂直于电场方向射入两平行板间的匀强电场中,P从两极板正中央射入,Q从下极板边缘处射入,它们最后打在同一点(重力不计),则从开始射入到打到上极板的过程中( )
如图所示,质量相同的两个带电粒子P、Q以相同的初速度沿垂直于电场方向射入两平行板间的匀强电场中,P从两极板正中央射入,Q从下极板边缘处射入,它们最后打在同一点(重力不计),则从开始射入到打到上极板的过程中( )| A. | 它们运动的时间tP:tQ=1:2 | |
| B. | 它们的电势能减少量之比△EP:△EQ=1:4 | |
| C. | 它们所带电荷量之比qp:qQ=1:2 | |
| D. | 它们的速度增量之比△vp:△vQ=1:2 |

| A. | Q2带负电且Q1与Q2的电荷量之比为4:9 | |
| B. | b点的电势一定为零 | |
| C. | b点的电场强度一定为零 | |
| D. | 粒子在a点的电势能比b点的电势能小 |
 在对《探究动能定理》实验进行下列改进:弹性绳两端固定,中间一布兜包小球,拉弹性绳达某一形变量时放手,小球沿水平光滑板从A点滑上光滑竖直平面内半径R=1m 的半圆,更换质量不同的小球保持弹性绳形变量相同,在B点处一传感器测出其压力FN大小随小球质量m变化情况如图2:
在对《探究动能定理》实验进行下列改进:弹性绳两端固定,中间一布兜包小球,拉弹性绳达某一形变量时放手,小球沿水平光滑板从A点滑上光滑竖直平面内半径R=1m 的半圆,更换质量不同的小球保持弹性绳形变量相同,在B点处一传感器测出其压力FN大小随小球质量m变化情况如图2: 质量为m、带电量为+q的微粒,沿与水平方向夹角为30o的方向射入某一匀强电场区域,如图所示.在图中虚线框内存在匀强电场.(重力加速度大小为g)
质量为m、带电量为+q的微粒,沿与水平方向夹角为30o的方向射入某一匀强电场区域,如图所示.在图中虚线框内存在匀强电场.(重力加速度大小为g) 如图所示,在方向水平向右的匀强电场中,一不可伸长的不导电细线的一端连着一个质量为m的带电小球,另一端固定于O点,当小球静止在B点时,细线与竖直方向夹角θ=30°问:
如图所示,在方向水平向右的匀强电场中,一不可伸长的不导电细线的一端连着一个质量为m的带电小球,另一端固定于O点,当小球静止在B点时,细线与竖直方向夹角θ=30°问: