题目内容
14.让一价的氢离子(电荷量为e、质量为m)、一价的氦离子(电荷量为e、质量为4m)、二价的氦离子(电荷量为2e、质量为4m)的混合物经过同一加速电场由静止开始加速,然后在同一偏转电场里偏转后离开偏转电场,不计重力及粒子间的相互作用,则( )| A. | 三个离子离开偏转电场时的速度方向相同 | |
| B. | 三个离子在偏转电场中的位移相等 | |
| C. | 一价的氢离子、一价的氦离子离开电场时的动能相等 | |
| D. | 三个离子同时离开偏转电场 |
分析 两种粒子在偏转电场中做类平抛运动,垂直于电场方向上做匀速直线运动,根据动能定理求出加速获得的速度表达式,可分析在偏转电场中经历的时间关系.根据推论分析粒子偏转距离与加速电压和偏转电压的关系,从而得出偏转位移的关系.
解答 解:A、D、设加速电压为U1,偏转电压为U2,偏转极板的长度为L,板间距离为d.
在加速电场中,由动能定理得:qU1=$\frac{1}{2}m{{v}_{0}}^{2}$得,加速获得的速度为v0=$\sqrt{\frac{2q{U}_{1}}{m}}$,两种粒子在偏转电场中,水平方向做速度为v0的匀速直线运动,由于两种粒子的比荷不同,则v0不同,所以两粒子在偏转电场中运动的时间不同.
两种粒子在加速电场中的加速度不同,位移相同,则运动的时间也不同,所以两粒子是先后离开偏转电场.
粒子离开偏转电场时,沿电场线方向的分速度:
${v}_{y}=at=\frac{q{U}_{2}}{md}•\frac{L}{{v}_{0}}$
速度的偏转角:$tanθ=\frac{{v}_{y}}{{v}_{0}}=\frac{q{U}_{2}}{md}•\frac{L}{{v}_{0}^{2}}$=$\frac{{U}_{2}L}{4d{U}_{1}}$,与电荷的电量和质量无关.三个离子离开偏转电场时的速度方向相同.故A正确,D错误;
B、在偏转电场中的偏转位移y=$\frac{1}{2}a{t}^{2}=\frac{1}{2}•\frac{q{U}_{2}}{md}\frac{{L}^{2}}{{{v}_{0}}^{2}}=\frac{{U}_{2}{L}^{2}}{4d{U}_{1}}$,与电荷的电量和质量无关.知出射点的位置相同.故B正确;
C、在偏转电场中偏转的过程中:${E}_{k}-\frac{1}{2}m{v}_{0}^{2}=q•E•y=\frac{q{U}_{2}}{d}•\frac{{U}_{2}{L}^{2}}{4d{U}_{1}}$,所以:粒子离开偏转电场时的动能:
${E}_{k}=q{U}_{1}+\frac{q{U}_{2}^{2}{L}^{2}}{4{d}^{2}{U}_{1}}$
粒子的动能与粒子的质量无关,与粒子的电量成正比,所以一价的氢离子、一价的氦离子离开电场时的动能相等.故C正确
故选:ABC
点评 解决本题的关键知道带电粒子在加速电场和偏转电场中的运动情况,知道从静止开始经过同一加速电场加速,垂直打入偏转电场,运动轨迹相同.

 如图所示,在一块足够大的铅板A的右侧固定着一小块放射源P,P向各个方向不断放射出电子,电子的初速度大小均为v0,电子的重力忽略不计.在A板右方距A为d处放置一个与A平行的金属板B,在A、B之间加上恒定电压U(B板电势高)( )
如图所示,在一块足够大的铅板A的右侧固定着一小块放射源P,P向各个方向不断放射出电子,电子的初速度大小均为v0,电子的重力忽略不计.在A板右方距A为d处放置一个与A平行的金属板B,在A、B之间加上恒定电压U(B板电势高)( )| A. | 电子打在B板上的范围是个圆 | |
| B. | 仅增加d的大小,电子到达B板时的动能增大 | |
| C. | 仅增加d的大小,电子打在B板时的范围面积增大 | |
| D. | 仅增加U的大小,电子打在B板时的范围面积不变 |
 如图所示,绝缘长方体B置于水平面上,两端固定一对平行带电极板,极极间形成匀强电场E,长方体B的上表面光滑,下表面与水平面间的动摩擦因数μ=0.05(设最大静摩擦力与滑动摩擦力相同),B与极板的总质量mB=1.0kg.带正电的小滑块A的质量mA=0.6kg,其受到的电场力大小F=1.2N.假设A所带的电荷量不影响极板间的电场分布.某时刻,小滑块A从B的上表面以速度vA向左运动,同时B(连同极板)以速度vB向右运动.g取10m/s2,则B刚开始运动时的加速度为( )
如图所示,绝缘长方体B置于水平面上,两端固定一对平行带电极板,极极间形成匀强电场E,长方体B的上表面光滑,下表面与水平面间的动摩擦因数μ=0.05(设最大静摩擦力与滑动摩擦力相同),B与极板的总质量mB=1.0kg.带正电的小滑块A的质量mA=0.6kg,其受到的电场力大小F=1.2N.假设A所带的电荷量不影响极板间的电场分布.某时刻,小滑块A从B的上表面以速度vA向左运动,同时B(连同极板)以速度vB向右运动.g取10m/s2,则B刚开始运动时的加速度为( )| A. | 2m/s2,方向水平向右 | B. | 2m/s2,方向水平向左 | ||
| C. | 0.8m/s2,方向水平向左 | D. | 0.05m/s2,方向水平向左 |
 如图所示,为一列沿x轴正方向传播的机械波在某一时刻的图象,由图可知,这列波的振幅A、波长λ和x=l米处质点的速度方向分别为( )
如图所示,为一列沿x轴正方向传播的机械波在某一时刻的图象,由图可知,这列波的振幅A、波长λ和x=l米处质点的速度方向分别为( )| A. | A=0.4 m λ=1m 向上 | B. | A=1 m λ=0.4m 向下 | ||
| C. | A=0.4 m λ=2m 向下 | D. | A=2 m λ=3m 向上 |

 如图所示,水平放置的平行板电容器,两板间距d=8cm,板长L=25cm,接在直流电源上.一个带电油滴以v0=0.5m/s的初速度从板间的正中央水平射入,恰好做匀速直线运动,当它运动到P处时迅速将下板向上提起△d=$\frac{4}{3}$cm,油滴刚好从金属板末端飞出,g取10m/s2.求:
如图所示,水平放置的平行板电容器,两板间距d=8cm,板长L=25cm,接在直流电源上.一个带电油滴以v0=0.5m/s的初速度从板间的正中央水平射入,恰好做匀速直线运动,当它运动到P处时迅速将下板向上提起△d=$\frac{4}{3}$cm,油滴刚好从金属板末端飞出,g取10m/s2.求: 如图甲所示,离子发生器能连续均匀地发射质量为m.电荷量为+q的离子.并从O点无初速进入间距为d1的两平行极板AB之间.离子穿过极板B上的小孔后,恰好沿两平行板MN间的中心线射入偏转电场.已知MN两板长均为L,MN两板间所加电压恒为U,且M板的电势高于N板电势.则:
如图甲所示,离子发生器能连续均匀地发射质量为m.电荷量为+q的离子.并从O点无初速进入间距为d1的两平行极板AB之间.离子穿过极板B上的小孔后,恰好沿两平行板MN间的中心线射入偏转电场.已知MN两板长均为L,MN两板间所加电压恒为U,且M板的电势高于N板电势.则: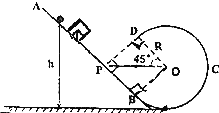 竖直平面内的直轨道AB与$\frac{3}{4}$圆弧形轨道BCD在B处相切,半径OD=R与水平方向成45°角,如图所示,整个轨道光滑绝缘,质量为m的带电小球从直轨道上某点由静止开始沿轨道下滑,当小球下滑到B点时,在空间加上水平向左的匀强电场,场强大小为E,小球恰能沿圆弧轨道运动,至D后沿直线DP垂直打在直轨道上的P点.
竖直平面内的直轨道AB与$\frac{3}{4}$圆弧形轨道BCD在B处相切,半径OD=R与水平方向成45°角,如图所示,整个轨道光滑绝缘,质量为m的带电小球从直轨道上某点由静止开始沿轨道下滑,当小球下滑到B点时,在空间加上水平向左的匀强电场,场强大小为E,小球恰能沿圆弧轨道运动,至D后沿直线DP垂直打在直轨道上的P点. 如图所示,光滑绝缘的半圆形轨道固定于竖直平面内,半圆形轨道与光滑绝缘的水平地面相切于半圆的端点A.一质量为1kg的小球在水平地面上匀速运动,速度为v=6m/s,经A运动到轨道最高点B,最后又落在水平地面上的D点(图中未画出).已知整个空间存在竖直向下的匀强电场,小球带正电荷,小球所受电场力的大小等于2mg,g为重力加速度.
如图所示,光滑绝缘的半圆形轨道固定于竖直平面内,半圆形轨道与光滑绝缘的水平地面相切于半圆的端点A.一质量为1kg的小球在水平地面上匀速运动,速度为v=6m/s,经A运动到轨道最高点B,最后又落在水平地面上的D点(图中未画出).已知整个空间存在竖直向下的匀强电场,小球带正电荷,小球所受电场力的大小等于2mg,g为重力加速度.