题目内容
15.已知地球半径为R,月球半径为r,地球与月球之间的距离(两中心之间的距离)为S.月球公转的周期为T1,地球自转的周期为T2,地球公转周期为T3,万有引力常量为G,由以上条件可知( )| A. | 地球的质量为m=$\frac{4{π}^{2}S}{G{{T}_{3}}^{2}}$ | B. | 月球的质量为m=$\frac{4{π}^{2}S}{G{{T}_{1}}^{2}}$ | ||
| C. | 地球的密度为ρ=$\frac{3πS}{G{{T}_{1}}^{2}}$ | D. | 月球运动的加速度为a=$\frac{4{π}^{2}S}{{{T}_{1}}^{2}}$ |
分析 研究月球绕地球圆周运动,利用万有引力提供向心力可求出地球的质量.
研究在地球表面附近运行的人造卫星,利用万有引力提供向心力可表示出地球的质量,从而求出密度.
解答 解:A、研究月球绕地球圆周运动,利用万有引力提供向心力得:
G$\frac{Mm}{{r}^{2}}$=mr$\frac{4{π}^{2}}{{T}_{1}^{2}}$
解得:M=$\frac{4{π}^{2}{S}^{3}}{G{T}_{1}^{2}}$,故A错误
B、由于不知道月球的卫星的相关量,故不能求得月球质量,故B错误
C、研究在地球表面附近运行的人造卫星,利用万有引力提供向心力:
G$\frac{Mm}{{R}^{2}}$=mR$\frac{4{π}^{2}}{{T}_{3}^{2}}$
又:ρ=$\frac{M}{V}$=$\frac{3π}{G{T}_{3}^{2}}$,故C错误
D、月球向心加速度为:a=sω2=s×($\frac{2π}{{T}_{1}}$)2=$\frac{4{π}^{2}S}{{T}_{1}^{2}}$,故D正确
故选:D
点评 解决本题的关键掌握万有引力提供向心力,注意不同的圆周运动对应不同的轨道半径和周期.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
5. 如图所示,V1、V2是理想电压表,当闭合开关,将滑动变阻器的触片由左端向右滑动时,下列说法中正确的是( )
如图所示,V1、V2是理想电压表,当闭合开关,将滑动变阻器的触片由左端向右滑动时,下列说法中正确的是( )
 如图所示,V1、V2是理想电压表,当闭合开关,将滑动变阻器的触片由左端向右滑动时,下列说法中正确的是( )
如图所示,V1、V2是理想电压表,当闭合开关,将滑动变阻器的触片由左端向右滑动时,下列说法中正确的是( )| A. | 小灯泡L2变暗,V1表的读数变小,V2表的读数变大 | |
| B. | 小灯泡L1变亮,V1表的读数变大,V2表的读数变小 | |
| C. | 小灯泡L2变亮,V1表的读数变大,V2表的读数变小 | |
| D. | 小灯泡L1变暗,V1表的读数变小,V2表的读数变大 |
10.下列有关高中物理实验的描述中,正确的是( )
| A. | 在“验证力的平行四边形定则”的实验中,拉橡皮筋的细绳要稍长,并且实验时要使弹簧测力计与木板平面平行,同时保证弹簧的轴线与细绳在同一直线上 | |
| B. | 在“研究平抛物体的运动”的实验中,必须要用秒表测出平抛物体的运动时间 | |
| C. | 在“验证动量守恒定律”实验中入射球的质量应大于被碰球的质量,入射球每次应从同一高度无初速度滑下 | |
| D. | 在“用油膜法测分子直径的大小”的实验中,需要用天平测油滴的质量 | |
| E. | 在“用单摆测定重力加速度”实验中,如果摆长测量无误.预得的g值偏小,其原因可能是将全振动的次数N误计为N+1 | |
| F. | 在“用电流场模拟静电场描绘电场的等势线”的实验中,要在木板上自上而下依次铺放白纸、复写纸、导电纸. |
20. 如图所示,地球球心为O,半径为R,表面的重力加速度为g.-宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )
如图所示,地球球心为O,半径为R,表面的重力加速度为g.-宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )
 如图所示,地球球心为O,半径为R,表面的重力加速度为g.-宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )
如图所示,地球球心为O,半径为R,表面的重力加速度为g.-宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )| A. | 飞船在P点的加速度一定是$\frac{g}{9}$ | |
| B. | 飞船经过P的速度一定是$\sqrt{\frac{gR}{3}}$ | |
| C. | 飞船经过P点的速度一定小于$\sqrt{\frac{gR}{3}}$ | |
| D. | 飞船经过P点时,对准地心弹射出的物体一定沿PO直线落向地面 |




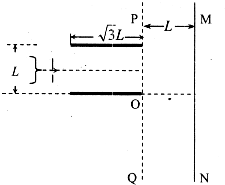 如图所示,-离子枪中,质量为、电荷量为的离子,经加速电场从静止加速后形成水平方向的离子柬射向两水平放置的平行金属板间,已知金属板长为、板间距为L、两板间电压为U,离子束沿两板间中线射入,不计重力,要使离子进入电场后由下金属板边缘O点射出,求:
如图所示,-离子枪中,质量为、电荷量为的离子,经加速电场从静止加速后形成水平方向的离子柬射向两水平放置的平行金属板间,已知金属板长为、板间距为L、两板间电压为U,离子束沿两板间中线射入,不计重力,要使离子进入电场后由下金属板边缘O点射出,求: 在光滑的水平面上,停着一辆平板小车,小车的质量为M=10kg.在小车左端A处放有质量为m=5kg的物体a(可视为质点),紧靠小车右脚有一个半径R=1.8m的四分之一光滑圆孤轨道,轨道下端水平,如图所示,现让一质量M1=10kg的小滑块b(可视为质点)从轨道顶端自由滑下与小车相撞,碰撞时间极短且没有机械能损失,已知物体a与平板车间的动摩擦因数μ=0.4,后来物体在平板车上相对于小车向右滑行L后被弹回,最后刚好在A点与车保持相对静止,g=10m/s2,求:
在光滑的水平面上,停着一辆平板小车,小车的质量为M=10kg.在小车左端A处放有质量为m=5kg的物体a(可视为质点),紧靠小车右脚有一个半径R=1.8m的四分之一光滑圆孤轨道,轨道下端水平,如图所示,现让一质量M1=10kg的小滑块b(可视为质点)从轨道顶端自由滑下与小车相撞,碰撞时间极短且没有机械能损失,已知物体a与平板车间的动摩擦因数μ=0.4,后来物体在平板车上相对于小车向右滑行L后被弹回,最后刚好在A点与车保持相对静止,g=10m/s2,求: 如图所示,竖直放置在水平面上的轻弹簧上放着质量为2kg的物体A,处于静止状态,将一个质量为3kg的物体B轻放在A上的瞬间,B对A的压力大小为(g取10m/s2)( )
如图所示,竖直放置在水平面上的轻弹簧上放着质量为2kg的物体A,处于静止状态,将一个质量为3kg的物体B轻放在A上的瞬间,B对A的压力大小为(g取10m/s2)( )