题目内容
20. 如图所示,地球球心为O,半径为R,表面的重力加速度为g.-宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )
如图所示,地球球心为O,半径为R,表面的重力加速度为g.-宇宙飞船绕地球无动力飞行且沿椭圆轨道运动,轨道上P点距地心最远,距离为3R.为研究方便,假设地球不自转且忽略空气阻力,则( )| A. | 飞船在P点的加速度一定是$\frac{g}{9}$ | |
| B. | 飞船经过P的速度一定是$\sqrt{\frac{gR}{3}}$ | |
| C. | 飞船经过P点的速度一定小于$\sqrt{\frac{gR}{3}}$ | |
| D. | 飞船经过P点时,对准地心弹射出的物体一定沿PO直线落向地面 |
分析 飞船在P点的加速度即为万有引力产生的加速度,根据万有引力加速度的表达式可知加速度的大小与距球心的距离平方成反比,从而求出P点的加速度与地球表面重力加速的大小关系;根据椭圆轨道上卫星运动从远地点开始将做近心运动,满足万有引力大于运动所需要的向心力,从而确定线速度的大小关系.
解答 解:A、在地球表面重力加速度与万有引力加速度相等,根据牛顿第二定律有:G$\frac{Mm}{{r}^{2}}$=ma,加速度a=$\frac{GM}{{r}^{2}}$,在地球表面有:g=$\frac{GM}{{R}^{2}}$,P点的加速度ap=$\frac{GM}{9{R}^{2}}=\frac{g}{9}$.故A正确.
B、在椭圆轨道上飞船从P点开始将做近心运动,此时满足万有引力大于P点所需向心力即:map>m$\frac{{V}_{P}^{2}}{3R}$,
如果飞船在P点绕地球做圆周运动时满足map=m$\frac{{V}^{2}}{3R}$,解得v=$\sqrt{\frac{gR}{3}}$,由此分析知:vp<$\sqrt{\frac{gR}{3}}$.故C正确,B错误.
D、飞船经过P点时,对准地心弹射出的物体,由于惯性,弹射出的物体与飞船具有相同的速度,物体的速度不沿地心方向,不会沿PO直线落向地面.故D错误.
故选:AC.
点评 解决本题的关键万有万有引力提供向心力这一重要理论,并能灵活运用,以及知道变轨的原理,抓住万有引力与向心力的大小关系进行判断.

练习册系列答案
相关题目
10. 一列平面简谐波,波速为20m/s,沿x轴正方向传播,在某一时刻这列波的图象如图所示.则下列说法错误的是( )
一列平面简谐波,波速为20m/s,沿x轴正方向传播,在某一时刻这列波的图象如图所示.则下列说法错误的是( )
 一列平面简谐波,波速为20m/s,沿x轴正方向传播,在某一时刻这列波的图象如图所示.则下列说法错误的是( )
一列平面简谐波,波速为20m/s,沿x轴正方向传播,在某一时刻这列波的图象如图所示.则下列说法错误的是( )| A. | 这列波的周期是0.2 s | |
| B. | 质点P、Q此时刻的运动方向都沿y轴正方向 | |
| C. | 质点P、R在任意时刻的位移都相同 | |
| D. | 质点P、S在任意时刻的速度都相同 |
8.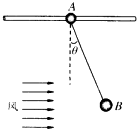 如图所示,水平细杆上套一A环,A环与B球间用一轻质绳相连,质量分别为mA、mB,由于B球受到风力作用,A环与B球一起向右匀速运动.已知细绳与竖直方向的夹角为θ,则下列说法中正确的是( )
如图所示,水平细杆上套一A环,A环与B球间用一轻质绳相连,质量分别为mA、mB,由于B球受到风力作用,A环与B球一起向右匀速运动.已知细绳与竖直方向的夹角为θ,则下列说法中正确的是( )
 如图所示,水平细杆上套一A环,A环与B球间用一轻质绳相连,质量分别为mA、mB,由于B球受到风力作用,A环与B球一起向右匀速运动.已知细绳与竖直方向的夹角为θ,则下列说法中正确的是( )
如图所示,水平细杆上套一A环,A环与B球间用一轻质绳相连,质量分别为mA、mB,由于B球受到风力作用,A环与B球一起向右匀速运动.已知细绳与竖直方向的夹角为θ,则下列说法中正确的是( )| A. | B球受到的风力F等于mBgtanθ | |
| B. | 风力增大时,轻质绳对B球的拉力保持不变 | |
| C. | 杆对A环的支持力随着风力的增加而增加 | |
| D. | A环与水平细杆间的动摩擦因数为$\frac{{m}_{B}}{{m}_{A}+{m}_{B}}$ |
15.已知地球半径为R,月球半径为r,地球与月球之间的距离(两中心之间的距离)为S.月球公转的周期为T1,地球自转的周期为T2,地球公转周期为T3,万有引力常量为G,由以上条件可知( )
| A. | 地球的质量为m=$\frac{4{π}^{2}S}{G{{T}_{3}}^{2}}$ | B. | 月球的质量为m=$\frac{4{π}^{2}S}{G{{T}_{1}}^{2}}$ | ||
| C. | 地球的密度为ρ=$\frac{3πS}{G{{T}_{1}}^{2}}$ | D. | 月球运动的加速度为a=$\frac{4{π}^{2}S}{{{T}_{1}}^{2}}$ |
12.在2010年温哥华冬奥会上,申雪和赵宏博在双人滑比赛中一举夺金.假设冰面对赵宏博的最大静摩擦力为重力的k倍则他在水平冰面上以速率v沿圆周滑行时的半径为( )
| A. | R≤$\frac{{v}^{2}}{kg}$ | B. | R≥$\frac{{v}^{2}}{kg}$ | C. | R≤$\frac{2{v}^{2}}{kg}$ | D. | R≥$\frac{{v}^{2}}{2kg}$ |
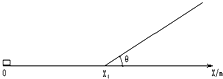 物体在水平面上从X轴坐标原点O以V0=20m/s的初速度沿X轴正方向开始运动,由X1=20m处滑上一个倾角为45°的斜面,又滑了下来,物体每次经过斜面底端时都不损失机械能.已知动摩擦因数均为μ=0.50,g取10m/s2.求:物体停止运动时位置的坐标.(计算结果保留三位有效数字)
物体在水平面上从X轴坐标原点O以V0=20m/s的初速度沿X轴正方向开始运动,由X1=20m处滑上一个倾角为45°的斜面,又滑了下来,物体每次经过斜面底端时都不损失机械能.已知动摩擦因数均为μ=0.50,g取10m/s2.求:物体停止运动时位置的坐标.(计算结果保留三位有效数字) 如图所示,质量分别为mA=3kg、mB=1kg的物块A、B置于足够长的水平面上,在F=13N的水平推力作用下,一起由静止开始向右做匀加速运动,已知A、B与水平面间的动摩擦因素分别为μA=0.1,μB=0.2,取g=10m/s2.求:
如图所示,质量分别为mA=3kg、mB=1kg的物块A、B置于足够长的水平面上,在F=13N的水平推力作用下,一起由静止开始向右做匀加速运动,已知A、B与水平面间的动摩擦因素分别为μA=0.1,μB=0.2,取g=10m/s2.求:
 如图所示,用一根轻质、光滑且不可伸长的绳子晾晒衣服,绳长L,绳子的两端分别固定在间距为d的两根竖直杆上(已知L>d),衣服及衣服撑的总质量为m,重力加速度为g,当利用衣服撑把衣服挂到此绳子上静止后,求此时绳子的张力大小.
如图所示,用一根轻质、光滑且不可伸长的绳子晾晒衣服,绳长L,绳子的两端分别固定在间距为d的两根竖直杆上(已知L>d),衣服及衣服撑的总质量为m,重力加速度为g,当利用衣服撑把衣服挂到此绳子上静止后,求此时绳子的张力大小.