题目内容
12.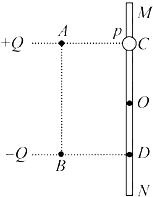 如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.则根据已知信息能定量得到的物理量是( )
如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.则根据已知信息能定量得到的物理量是( )| A. | O点处的电场强度E | |
| B. | C、O间的电势差UCO | |
| C. | 小球p经过与点电荷B等高的D点时的速度V | |
| D. | 小球p在向下运动中C至D的时间T |
分析 由点电荷的场强公式结合平行四边形定则求解;对C到O段运用动能定理,求出C、O间的电势差,再求出C、D间的电势差UCD;由电场的对称性知,UOD=UCO,小球从O到D由动能定理求小球p经过与点电荷B等高的D点时的速度.
解答 解:A、点电荷A(或B)在O点处产生的场强大小为:$E′=\frac{kQ}{{{{(\sqrt{2}d)}^2}}}=\frac{kQ}{{2{d^2}}}$;
根据平行四边形定则,O点处的电场强度:$E=\sqrt{2}E′=\frac{\sqrt{2}k{Q}^{2}}{{2d}^{2}}$;故A正确;
B、小球从C运动到O(动能定理)得:$mgd+{U_{CO}}•q=\frac{1}{2}m{v^2}-0$,解得:${U_{CO}}=\frac{{m{v^2}-2mgd}}{2q}$,故B正确;
C、结合对称性,CO间电势差与OD间电势差相等;可以对从C到D过程根据动能定理列式得到小球p经过与点电荷B等高的D点时的速度,故C正确;
D、由于是变加速运动,故无法求解运动的时间,故D错误;
故选:ABC.
点评 本题关键要正确分析小球的受力情况,运用牛顿第二定律、动能定理处理力电综合问题,分析要知道O点的场强实际上是两点电荷在O点产生场强的合场强,等量异种电荷的电场具有对称性.

练习册系列答案
相关题目
12.暗物质是二十一世纪物理学之谜,对该问题的研究可能带来一场物理学的革命.为了探测暗物质,我国在2015年12月17日成功发射了一颗被命名为“悟空”的暗物质探测卫星.已知“悟空”在低于同步卫星的轨道上绕地球做匀速圆周运动,同时地球同步轨道上还有一与“悟空”质量相等的卫星,则下列说法正确的是( )
| A. | “悟空”的线速度大于第一宇宙速度 | |
| B. | “悟空”的向心加速度大于地球同步轨道上卫星的向心加速度 | |
| C. | “悟空”的动能大于地球同步轨道上卫星的动能 | |
| D. | “悟空”和地球同步轨道上的卫星与地心的连线在单位时间内扫过的面积相等 |
13. 如图所示,图中的实线是一簇未标明方向的由点电荷产生的电场线,虚线是某带电粒子在电场中从a到b的运动轨迹,若带电粒子在运动中只受电场力作用,根据此图能不做出正确判断的是( )
如图所示,图中的实线是一簇未标明方向的由点电荷产生的电场线,虚线是某带电粒子在电场中从a到b的运动轨迹,若带电粒子在运动中只受电场力作用,根据此图能不做出正确判断的是( )
 如图所示,图中的实线是一簇未标明方向的由点电荷产生的电场线,虚线是某带电粒子在电场中从a到b的运动轨迹,若带电粒子在运动中只受电场力作用,根据此图能不做出正确判断的是( )
如图所示,图中的实线是一簇未标明方向的由点电荷产生的电场线,虚线是某带电粒子在电场中从a到b的运动轨迹,若带电粒子在运动中只受电场力作用,根据此图能不做出正确判断的是( )| A. | 带电粒子在a、b两点的受力方向 | |
| B. | 带电粒子在a、b两点的加速度何处比较大 | |
| C. | 带电粒子在a、b两点的速度何处比较大 | |
| D. | 带电粒子所带电荷的电性 |
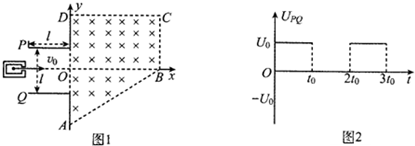
4. 如图所示,在一平面正方形MNPQ区域内有一匀强磁场垂直于纸面向里,磁感应强度为B.一质量为m、电荷量为q的粒子以速度v从Q点沿着与边QP夹角为30°的方向垂直进入磁场,从QP边界射出.已知QP边长为a,不计粒子的重力,下列说法正确的是( )
如图所示,在一平面正方形MNPQ区域内有一匀强磁场垂直于纸面向里,磁感应强度为B.一质量为m、电荷量为q的粒子以速度v从Q点沿着与边QP夹角为30°的方向垂直进入磁场,从QP边界射出.已知QP边长为a,不计粒子的重力,下列说法正确的是( )
 如图所示,在一平面正方形MNPQ区域内有一匀强磁场垂直于纸面向里,磁感应强度为B.一质量为m、电荷量为q的粒子以速度v从Q点沿着与边QP夹角为30°的方向垂直进入磁场,从QP边界射出.已知QP边长为a,不计粒子的重力,下列说法正确的是( )
如图所示,在一平面正方形MNPQ区域内有一匀强磁场垂直于纸面向里,磁感应强度为B.一质量为m、电荷量为q的粒子以速度v从Q点沿着与边QP夹角为30°的方向垂直进入磁场,从QP边界射出.已知QP边长为a,不计粒子的重力,下列说法正确的是( )| A. | 该粒子带正电 | B. | 运动过程中粒子的速度不变 | ||
| C. | 粒子在磁场中运动的时间为$\frac{mπ}{3qB}$ | D. | 粒子的速度v的最大值为$\frac{qBa}{2m}$ |
1.在下列学生实验中,需要用到打点计时器的实验有( )
| A. | “探究求合力的方法” | B. | “探究加速度与力、质量的关系” | ||
| C. | “探究做功与物体速度变化的关系” | D. | “探究作用力与反作用力的关系” |
2. 如图所示,光滑平行的金属导轨水平放置,间距L=0.2m,其左端接有R=1Ω的定值电阻,磁感应强度大小为B=0.5T的匀强磁场垂直于导轨平面向下.导体棒MN垂直静置在导轨上,不计导轨和导体棒的电阻.在平行于导轨的变力F=1+0.1t(N)的作用下,导体棒由静止开始向右做匀加速运动,运动过程中导体棒与导轨始终接触良好,则下列说法中正确的是( )
如图所示,光滑平行的金属导轨水平放置,间距L=0.2m,其左端接有R=1Ω的定值电阻,磁感应强度大小为B=0.5T的匀强磁场垂直于导轨平面向下.导体棒MN垂直静置在导轨上,不计导轨和导体棒的电阻.在平行于导轨的变力F=1+0.1t(N)的作用下,导体棒由静止开始向右做匀加速运动,运动过程中导体棒与导轨始终接触良好,则下列说法中正确的是( )
 如图所示,光滑平行的金属导轨水平放置,间距L=0.2m,其左端接有R=1Ω的定值电阻,磁感应强度大小为B=0.5T的匀强磁场垂直于导轨平面向下.导体棒MN垂直静置在导轨上,不计导轨和导体棒的电阻.在平行于导轨的变力F=1+0.1t(N)的作用下,导体棒由静止开始向右做匀加速运动,运动过程中导体棒与导轨始终接触良好,则下列说法中正确的是( )
如图所示,光滑平行的金属导轨水平放置,间距L=0.2m,其左端接有R=1Ω的定值电阻,磁感应强度大小为B=0.5T的匀强磁场垂直于导轨平面向下.导体棒MN垂直静置在导轨上,不计导轨和导体棒的电阻.在平行于导轨的变力F=1+0.1t(N)的作用下,导体棒由静止开始向右做匀加速运动,运动过程中导体棒与导轨始终接触良好,则下列说法中正确的是( )| A. | 导体棒的质量为1 kg | |
| B. | 导体棒的质量为0.1 kg | |
| C. | 导体棒的加速度为1 m/s2 | |
| D. | 导体棒由静止开始运动10 s过程通过定值电阻的电荷量为50 C |
 如图所示,一个竖直放置的气缸内壁光滑且导热良好,其横截面积为S,上端封闭,下端开口.两个不漏气的活塞A和B把气缸分为上下两部分气室.上部气室高度H上为0.5m,气室内气体压强为$\frac{P}{2}$;下部气室高度H下也为0.5m,气室内气体压强为P.气缸内气体可看作是理想气体.问:
如图所示,一个竖直放置的气缸内壁光滑且导热良好,其横截面积为S,上端封闭,下端开口.两个不漏气的活塞A和B把气缸分为上下两部分气室.上部气室高度H上为0.5m,气室内气体压强为$\frac{P}{2}$;下部气室高度H下也为0.5m,气室内气体压强为P.气缸内气体可看作是理想气体.问: