题目内容
4. 如图所示,在一平面正方形MNPQ区域内有一匀强磁场垂直于纸面向里,磁感应强度为B.一质量为m、电荷量为q的粒子以速度v从Q点沿着与边QP夹角为30°的方向垂直进入磁场,从QP边界射出.已知QP边长为a,不计粒子的重力,下列说法正确的是( )
如图所示,在一平面正方形MNPQ区域内有一匀强磁场垂直于纸面向里,磁感应强度为B.一质量为m、电荷量为q的粒子以速度v从Q点沿着与边QP夹角为30°的方向垂直进入磁场,从QP边界射出.已知QP边长为a,不计粒子的重力,下列说法正确的是( )| A. | 该粒子带正电 | B. | 运动过程中粒子的速度不变 | ||
| C. | 粒子在磁场中运动的时间为$\frac{mπ}{3qB}$ | D. | 粒子的速度v的最大值为$\frac{qBa}{2m}$ |
分析 粒子在磁场中做匀速圆周运动洛伦兹力提供向心力,根据粒子偏转方向确定粒子所受洛伦兹力方向,然后由左手定则判断出粒子的电性;
根据题意求出粒子在磁场中转过的圆心角,然后根据粒子周期公式求出粒子的运动时间;
粒子从P点射出时速度最大,求出粒子从P点射出时的轨道半径,然后应用牛顿第二定律求出粒子的最大速度.
解答 解:A、粒子从PQ边射出磁场,粒子刚射入磁场时受到的洛伦兹力垂直与速度斜向右下方,由左手定则可知,粒子带负电,故A错误;
B、粒子在磁场中做匀速圆周运动,粒子速度大小不变当方向发生变化,粒子速度发生变化,故B错误;
C、粒子在磁场中转过的圆心角:θ=2×30°=60°,粒子在磁场中的运动时间:t=$\frac{θ}{360°}$T=$\frac{60°}{360°}$×$\frac{2πm}{qB}$=$\frac{πm}{3qB}$,故C正确;
D、粒子从P点射出磁场时轨道半径最大,粒子速度最大,此时粒子轨道半径:r=a,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,粒子的最大速度:v=$\frac{qBr}{m}$=$\frac{qBa}{m}$,故D错误;
故选:C.
点评 粒子在磁场中做匀速圆周运动,粒子转过的圆心角等于弦切角的2倍,根据几何知识求出粒子转过的圆心角、轨道半径,然后应用牛顿第二定律与粒子做圆周运动的周期公式可以解题.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 简谐运动的周期和振幅无关 | |
| B. | 在弹簧振子做简谐运动的回复力表达式F=-kx中,F为振动物体所受的合外力,k为弹簧的进度系数 | |
| C. | 在波的传播方向上,某个质点的振动速度就是波的传播速度 | |
| D. | 在双缝干涉实验中,同种条件下用紫光做实验比红光做实验得到的条纹更宽 | |
| E. | 在单缝衍射现象中要产生明显的衍射现象,狭缝宽度必需比波长小或者相差不多 |
12.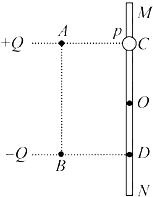 如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.则根据已知信息能定量得到的物理量是( )
如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.则根据已知信息能定量得到的物理量是( )
 如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.则根据已知信息能定量得到的物理量是( )
如图所示,固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷,电荷量分别为+Q和-Q,A、B相距为2d.MN是竖直放置的光滑绝缘细杆,另有一个穿过细杆的带电小球p,质量为m、电荷量为+q(可视为点电荷,不影响电场的分布),现将小球p从与点电荷A等高的C处由静止开始释放,小球p向下运动到距C点距离为d的O点时,速度为v.已知MN与AB之间的距离为d,静电力常量为k,重力加速度为g.则根据已知信息能定量得到的物理量是( )| A. | O点处的电场强度E | |
| B. | C、O间的电势差UCO | |
| C. | 小球p经过与点电荷B等高的D点时的速度V | |
| D. | 小球p在向下运动中C至D的时间T |
19. 在竖直方向的电场中一带电小球由静止开始竖直向上运动,运动过程中小球的机械能E与其位移S关系的图象如图所示,其中0~S1过程的图线为曲线,S1~S2过程中的图线为直线.根据该E-S图象,下列说法正确的是( )
在竖直方向的电场中一带电小球由静止开始竖直向上运动,运动过程中小球的机械能E与其位移S关系的图象如图所示,其中0~S1过程的图线为曲线,S1~S2过程中的图线为直线.根据该E-S图象,下列说法正确的是( )
 在竖直方向的电场中一带电小球由静止开始竖直向上运动,运动过程中小球的机械能E与其位移S关系的图象如图所示,其中0~S1过程的图线为曲线,S1~S2过程中的图线为直线.根据该E-S图象,下列说法正确的是( )
在竖直方向的电场中一带电小球由静止开始竖直向上运动,运动过程中小球的机械能E与其位移S关系的图象如图所示,其中0~S1过程的图线为曲线,S1~S2过程中的图线为直线.根据该E-S图象,下列说法正确的是( )| A. | 小球一定带正电 | |
| B. | 0~S1过程中小球始终在做加速直线运动 | |
| C. | S1~S2过程中小球的动能一定不断增大 | |
| D. | S1~S2过程中所处的电场一定是匀强电场 |
16.如图所示电场中A、B两点,则下列说法正确的是( )


| A. | 电势φA>φB,场强EA>EB | |
| B. | 电势φA>φB,场强EA<EB | |
| C. | 将电荷+q从A点移到B点静电力做了负功 | |
| D. | 将电荷-q分别放在A、B两点时具有的电势能EpA>EpB |
13.在探究功与速度变化量的关系的实验中橡皮筋释放后,关于小车的运动,下列说法正确的是( )
| A. | 一直做匀速直线运动 | |
| B. | 先做匀加速直线运动,再做匀速直线运动 | |
| C. | 先做加速度减小的变加速直线运动,再做匀速直线运动 | |
| D. | 先做加速度增大的变加速直线运动,再做匀速直线运动 |


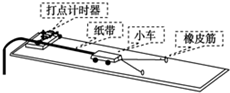 用如图所示的仪器探究做功与速度变化的关系.
用如图所示的仪器探究做功与速度变化的关系. 如图所示,两块平行金属极板MN水平放置,板长L=1m,间距d=$\frac{\sqrt{3}}{3}$m,两金属板间电压UMN=1×104V;在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域,正三角形ABC内存在垂直纸面向里的匀强磁场B1,三角形的上顶点A与上金属板M平齐,BC边与金属板平行,AB边的中点P恰好在下金属板N的右端点;正三角形FGH内存在垂直纸面向外的匀强磁场B2,已知A、F、G处于同一直线上,B、C、H也处于同一直线上,AF两点距离为$\frac{2}{3}$m.现从平行金属极板MN左端沿中心轴线方向入射一个重力不计的带电粒子,粒子质量m=3×10-10kg,带电量q=+1×10-4C,初速度v0=1×105m/s.
如图所示,两块平行金属极板MN水平放置,板长L=1m,间距d=$\frac{\sqrt{3}}{3}$m,两金属板间电压UMN=1×104V;在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域,正三角形ABC内存在垂直纸面向里的匀强磁场B1,三角形的上顶点A与上金属板M平齐,BC边与金属板平行,AB边的中点P恰好在下金属板N的右端点;正三角形FGH内存在垂直纸面向外的匀强磁场B2,已知A、F、G处于同一直线上,B、C、H也处于同一直线上,AF两点距离为$\frac{2}{3}$m.现从平行金属极板MN左端沿中心轴线方向入射一个重力不计的带电粒子,粒子质量m=3×10-10kg,带电量q=+1×10-4C,初速度v0=1×105m/s.