题目内容
2.若银河系外X恒星有一行星P围绕X恒星运行的周期为T1,它与X恒星中心的距离为月球到地球中心距离的n倍,月球绕地球运行郁周期为T2,假定行星P绕X恒星运行和月球绕地球运行均做匀速圆周运动,则下列说法正确的是( )| A. | X恒星质量与地球质量之比为$\frac{n{{T}_{2}}^{2}}{{{T}_{1}}^{2}}$ | |
| B. | X恒星质量与地球质量之比为$\frac{{n}^{3}{{T}_{2}}^{2}}{{{T}_{1}}^{2}}$ | |
| C. | 行星P运行速度与月球公转速度之比为$\frac{1}{\sqrt{n}}$ | |
| D. | 行星P运行速度与月球公转速度之比为$\frac{n{T}_{2}}{{T}_{1}}$ |
分析 根据万有引力提供向心力,求出中心天体质量的表达式,结合环绕天体轨道半径之比和周期之比求出中心天体的质量之比,结合轨道半径之比和周期之比求出公转速度之比.
解答 解:A、根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得,M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$,因为行星P绕恒星X的周期与月球绕地球的周期之比为$\frac{{T}_{1}}{{T}_{2}}$,行星P的轨道半径是月球轨道半径的n倍,则X恒星的质量与地球质量之比为$\frac{{n}^{3}{{T}_{2}}^{2}}{{{T}_{1}}^{2}}$,故B正确,A错误.
C、根据v=$\frac{2πr}{T}$知,行星P绕恒星X的周期与月球绕地球的周期之比为$\frac{{T}_{1}}{{T}_{2}}$,行星P的轨道半径是月球轨道半径的n倍,则行星P的运行速度与月球公转速度之比为$\frac{n{T}_{2}}{{T}_{1}}$,故D正确,C错误.
故选:BD.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,求出中心天体质量的表达式是解决本题的突破口,难度不大.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
12. 如图所示,长为L的水平板间有垂直纸面向内的匀强磁场,磁感应强度为B,板间距离也为L,板不带电,现有质量为m,电量为q的带正电粒子(不计重力和粒子间的相互作用力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子打在极板上,可采用的办法是( )
如图所示,长为L的水平板间有垂直纸面向内的匀强磁场,磁感应强度为B,板间距离也为L,板不带电,现有质量为m,电量为q的带正电粒子(不计重力和粒子间的相互作用力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子打在极板上,可采用的办法是( )
 如图所示,长为L的水平板间有垂直纸面向内的匀强磁场,磁感应强度为B,板间距离也为L,板不带电,现有质量为m,电量为q的带正电粒子(不计重力和粒子间的相互作用力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子打在极板上,可采用的办法是( )
如图所示,长为L的水平板间有垂直纸面向内的匀强磁场,磁感应强度为B,板间距离也为L,板不带电,现有质量为m,电量为q的带正电粒子(不计重力和粒子间的相互作用力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子打在极板上,可采用的办法是( )| A. | 使粒子的速度v=$\frac{3BqL}{2m}$ | B. | 使粒子的速度v=$\frac{BqL}{2m}$ | ||
| C. | 使粒子的速度v=$\frac{3BqL}{4m}$ | D. | 使粒子的速度v=$\frac{BqL}{5m}$ |
17.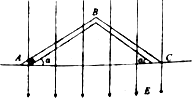 如图所示,一个“V”形玻璃管ABC倒置于平面内,并处于场强大小为E=1×103V/m,方向竖直向下的匀强电场中,一个重力为G=1×10-3N,电荷量为q=2×10-4C的带负电小滑块从A点由静止开始运动,小滑块与管壁的动摩擦因数μ=0.5.已知管长AB=BC=L=2m,倾角α=37°,B点是一段很短的光滑圆弧管,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法中正确的是( )
如图所示,一个“V”形玻璃管ABC倒置于平面内,并处于场强大小为E=1×103V/m,方向竖直向下的匀强电场中,一个重力为G=1×10-3N,电荷量为q=2×10-4C的带负电小滑块从A点由静止开始运动,小滑块与管壁的动摩擦因数μ=0.5.已知管长AB=BC=L=2m,倾角α=37°,B点是一段很短的光滑圆弧管,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法中正确的是( )
 如图所示,一个“V”形玻璃管ABC倒置于平面内,并处于场强大小为E=1×103V/m,方向竖直向下的匀强电场中,一个重力为G=1×10-3N,电荷量为q=2×10-4C的带负电小滑块从A点由静止开始运动,小滑块与管壁的动摩擦因数μ=0.5.已知管长AB=BC=L=2m,倾角α=37°,B点是一段很短的光滑圆弧管,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法中正确的是( )
如图所示,一个“V”形玻璃管ABC倒置于平面内,并处于场强大小为E=1×103V/m,方向竖直向下的匀强电场中,一个重力为G=1×10-3N,电荷量为q=2×10-4C的带负电小滑块从A点由静止开始运动,小滑块与管壁的动摩擦因数μ=0.5.已知管长AB=BC=L=2m,倾角α=37°,B点是一段很短的光滑圆弧管,sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,下列说法中正确的是( )| A. | B、A两点间的电势差为2000V | |
| B. | 小滑块从A点第一次运动到B点的过程中电势能增大 | |
| C. | 小滑块第一次速度为零的位置在C处 | |
| D. | 从开始运动到最后静止,小滑块通过的总路程为3m |
7. 如图所示,质量为m的物块置于质量为M的斜面上,物块和斜面都处于静止状态,给物块施加一水平向右的恒力F,物块和斜面仍处于静止状态,则( )
如图所示,质量为m的物块置于质量为M的斜面上,物块和斜面都处于静止状态,给物块施加一水平向右的恒力F,物块和斜面仍处于静止状态,则( )
 如图所示,质量为m的物块置于质量为M的斜面上,物块和斜面都处于静止状态,给物块施加一水平向右的恒力F,物块和斜面仍处于静止状态,则( )
如图所示,质量为m的物块置于质量为M的斜面上,物块和斜面都处于静止状态,给物块施加一水平向右的恒力F,物块和斜面仍处于静止状态,则( )| A. | 施加恒力后,物块与斜面间的弹力保持不变 | |
| B. | 施加恒力后,地面与斜面的支持力小于(M+m)g | |
| C. | 施加恒力后,物块与斜面间的摩擦力变小 | |
| D. | 施加恒力后,地面与斜面间的摩擦力大小为F |
14.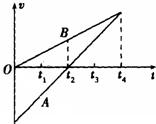 在一条宽马路上有A、B两车,在t=0时刻,两车刚好处于同一地点,接下来它们运动图象如图所示,那么,在0~t4时间内的情景是( )
在一条宽马路上有A、B两车,在t=0时刻,两车刚好处于同一地点,接下来它们运动图象如图所示,那么,在0~t4时间内的情景是( )
 在一条宽马路上有A、B两车,在t=0时刻,两车刚好处于同一地点,接下来它们运动图象如图所示,那么,在0~t4时间内的情景是( )
在一条宽马路上有A、B两车,在t=0时刻,两车刚好处于同一地点,接下来它们运动图象如图所示,那么,在0~t4时间内的情景是( )| A. | A车在0~t2时间内做匀加速直线运动,在t2时刻改变运动方向 | |
| B. | 在t2时刻A车速度为零,然后反向运动,此时两车相距最远 | |
| C. | 在t4时刻,A车追上B车 | |
| D. | 在t4时刻,两车相距最远 |
 (量程为0.6A,内阻约为0.25Ω)
(量程为0.6A,内阻约为0.25Ω) (量程为3A,内阻约为0.05Ω)
(量程为3A,内阻约为0.05Ω) (量程为3V,内阻约为3kΩ)
(量程为3V,内阻约为3kΩ) (量程为15V,内阻约为15kΩ)
(量程为15V,内阻约为15kΩ)
 某同学想测出银川当地的重力加速度g.为了减小误差,他设计了一个实验如下:将一根长直铝棒用细线悬挂在空中(如图甲所示),在靠近铝棒下端的一侧固定电动机M,使电动机转轴处于竖直方向,在转轴上水平固定一支特制笔N,借助转动时的现象,将墨汁甩出形成一条细线.调整笔的位置,使墨汁在棒上能清晰地留下墨线.启动电动机待转速稳定后,用火烧断悬线,让铝棒自由下落,笔在铝棒上相应位置留下墨线.
某同学想测出银川当地的重力加速度g.为了减小误差,他设计了一个实验如下:将一根长直铝棒用细线悬挂在空中(如图甲所示),在靠近铝棒下端的一侧固定电动机M,使电动机转轴处于竖直方向,在转轴上水平固定一支特制笔N,借助转动时的现象,将墨汁甩出形成一条细线.调整笔的位置,使墨汁在棒上能清晰地留下墨线.启动电动机待转速稳定后,用火烧断悬线,让铝棒自由下落,笔在铝棒上相应位置留下墨线.