题目内容
16.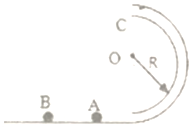 如图所示,半径R=0.2m,内径很小的光滑半圆管竖直固定放置,质量分别为m、2m的小球A和B(可看做质点)静止与光滑轨道的水平部分(小球的直径略小于半圆管的内径),现给小球一水平向右的初速度使其与小球A发生正碰,碰后A球通过最高点C时,对外管壁的压力大小为3mg,B球通过最高点C时,对内管壁的压力大小为mg,取g=10m/s2,求:
如图所示,半径R=0.2m,内径很小的光滑半圆管竖直固定放置,质量分别为m、2m的小球A和B(可看做质点)静止与光滑轨道的水平部分(小球的直径略小于半圆管的内径),现给小球一水平向右的初速度使其与小球A发生正碰,碰后A球通过最高点C时,对外管壁的压力大小为3mg,B球通过最高点C时,对内管壁的压力大小为mg,取g=10m/s2,求:(1)A、B两球落地点距C点水平距离之比;
(2)B球与A球碰撞前B球的速度大小.
分析 (1)小球在管道内做圆周运动,应用牛顿第二定律可以求出小球在C点的速度,小球离开C点后做平抛运动,应用平抛运动规律可以求出两球落点到C点的水平距离之比.
(2)由动能定理可以求出两球碰撞后的速度,两球碰撞过程过程系统动量守恒,应用动量守恒定律可以求出碰撞前B的速度大小.
解答 解:点,由牛顿第二定律得:
A球:mg+FA=m$\frac{{v}_{A}^{2}}{R}$,
B球:2mg-FB=2m$\frac{{v}_{B}^{2}}{R}$,
由题意可知:FA=3mg,FB=mg,
解得:vA=2$\sqrt{2}$m/s,vB=1m/s,
A、B两球通过最高点后做平抛运动,
由于抛出点的高度h相同,则它们的运动时间t相等,
设A、B两球落地点距C点水平距离分别为xA、xB,
则:xA=vAt,xB=vBt
解得:xA:xB=2$\sqrt{2}$:1;
(2)碰撞后A球、B球两球到达C点过程,由动能定理得:
对A球:-mg•2R=$\frac{1}{2}$mvA2-$\frac{1}{2}$mva2
解得:va=4m/s,
对B球:-2mg•2R=$\frac{1}{2}$•2mvB2-$\frac{1}{2}$•2mvb2
解得:vb=3m/s,
B球与A球碰撞过程系统动量守恒,以向右为正方向,
由动量守恒定律得:2mv0=2mvb+mva
解得:v0=5m/s;
答:(1)A、B两球落地点距C点水平距离之比为2$\sqrt{2}$:1;
(2)B球与A球碰撞前B球的速度大小为5m/s.
点评 本题考查了动能定理、牛顿第二定律与动量守恒定律的应用,分析清楚小球运动过程是解题的前提与关键,应用动能定理、牛顿第二定律与动量守恒定律可以解题,应用动量守恒定律解题时要注意正方向的选择.

练习册系列答案
相关题目
10. 如图竖直面内有一半径R=0.4m光滑半圆轨道,圆心在O点,BOD在同一竖直线上,圆弧在B点与水平传送带相切,水平传送带逆时针运动,速度大小为3m/s,AB长L=2m,将质量m=1kg的小滑块从A点由静止释放,滑块与皮带间动摩擦因数为0.4,g取10m/s2,下列说法正确的是( )
如图竖直面内有一半径R=0.4m光滑半圆轨道,圆心在O点,BOD在同一竖直线上,圆弧在B点与水平传送带相切,水平传送带逆时针运动,速度大小为3m/s,AB长L=2m,将质量m=1kg的小滑块从A点由静止释放,滑块与皮带间动摩擦因数为0.4,g取10m/s2,下列说法正确的是( )
 如图竖直面内有一半径R=0.4m光滑半圆轨道,圆心在O点,BOD在同一竖直线上,圆弧在B点与水平传送带相切,水平传送带逆时针运动,速度大小为3m/s,AB长L=2m,将质量m=1kg的小滑块从A点由静止释放,滑块与皮带间动摩擦因数为0.4,g取10m/s2,下列说法正确的是( )
如图竖直面内有一半径R=0.4m光滑半圆轨道,圆心在O点,BOD在同一竖直线上,圆弧在B点与水平传送带相切,水平传送带逆时针运动,速度大小为3m/s,AB长L=2m,将质量m=1kg的小滑块从A点由静止释放,滑块与皮带间动摩擦因数为0.4,g取10m/s2,下列说法正确的是( )| A. | 滑块刚进入圆弧轨道时对轨道压力为10N | |
| B. | 滑块在C点对轨道的压力为2.5N | |
| C. | 若只减小滑块质量,滑块到达C点时速度不变 | |
| D. | 若传送带速度足够大,小滑块一定能通过D点 |
11. 如图所示,在光滑水平面上,一小球在细线的拉力作用下,以角速度ω做半径为r的匀速圆周运动.则小球的向心加速度大小为( )
如图所示,在光滑水平面上,一小球在细线的拉力作用下,以角速度ω做半径为r的匀速圆周运动.则小球的向心加速度大小为( )
 如图所示,在光滑水平面上,一小球在细线的拉力作用下,以角速度ω做半径为r的匀速圆周运动.则小球的向心加速度大小为( )
如图所示,在光滑水平面上,一小球在细线的拉力作用下,以角速度ω做半径为r的匀速圆周运动.则小球的向心加速度大小为( )| A. | ωr | B. | ω2r | C. | $\frac{{ω}^{2}}{r}$ | D. | ωr2 |
1. 如图所示,在固定的光滑水平杆上,质量为m的物体P用细线跨过光滑的滑轮OO′连接质量为2m的物体Q,用手托住Q使整个系统静止,此时轻绳刚好拉直,且AO=L,OB=h,AB<BO',重力加速度为g;释放Q,让二者开始运动,则下列说法正确的是 ( )
如图所示,在固定的光滑水平杆上,质量为m的物体P用细线跨过光滑的滑轮OO′连接质量为2m的物体Q,用手托住Q使整个系统静止,此时轻绳刚好拉直,且AO=L,OB=h,AB<BO',重力加速度为g;释放Q,让二者开始运动,则下列说法正确的是 ( )
 如图所示,在固定的光滑水平杆上,质量为m的物体P用细线跨过光滑的滑轮OO′连接质量为2m的物体Q,用手托住Q使整个系统静止,此时轻绳刚好拉直,且AO=L,OB=h,AB<BO',重力加速度为g;释放Q,让二者开始运动,则下列说法正确的是 ( )
如图所示,在固定的光滑水平杆上,质量为m的物体P用细线跨过光滑的滑轮OO′连接质量为2m的物体Q,用手托住Q使整个系统静止,此时轻绳刚好拉直,且AO=L,OB=h,AB<BO',重力加速度为g;释放Q,让二者开始运动,则下列说法正确的是 ( )| A. | P物体从A点运动到O′的过程中,P、Q速度都在增大 | |
| B. | 在P物体从A滑到B的过程中,P的机械能增加、Q的机械能减小 | |
| C. | P运动的最大速度为$\sqrt{g(L-h)}$ | |
| D. | 当物体P到达B点时,物体Q减少的机械能为2mg(L-h) |
8.下列说法中正确的是 ( )
| A. | 声波从空气中传入水中时频率不变,波长变长 | |
| B. | 做简谐运动的质点,离开平衡位置的位移相同时,加速度也相同 | |
| C. | 双缝干涉实验中,若只减小双缝到光屏间的距离,两相邻条纹间距将变大 | |
| D. | 电磁波在真空中自由传播时,其传播方向与电场强度、磁感应强度方向均垂直 | |
| E. | 电磁波可以电磁振荡产生,若波源的电磁振荡停止,空间的电磁波随即消失 |
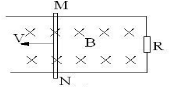 如图所示,在磁感应强度B=5T的匀强磁场中,垂直于磁场方向水平放置着两根相距为L=0.1m的平行光滑金属导轨,导轨的电阻忽略不计.在两根导轨的端点之间连接一阻值R=3Ω的电阻,导轨上跨放着一根电阻r=2Ω的金属棒MN,金属棒与导轨正交,当金属棒MN在外力作用下以速度v=4.0m/s向左做匀速运动时,试求:
如图所示,在磁感应强度B=5T的匀强磁场中,垂直于磁场方向水平放置着两根相距为L=0.1m的平行光滑金属导轨,导轨的电阻忽略不计.在两根导轨的端点之间连接一阻值R=3Ω的电阻,导轨上跨放着一根电阻r=2Ω的金属棒MN,金属棒与导轨正交,当金属棒MN在外力作用下以速度v=4.0m/s向左做匀速运动时,试求:
 蜘蛛虽有8只眼睛,但视力很差,完全靠感觉来捕食和生活,它的腿能敏捷地感觉到丝网的振动,如图所示为丝网做受迫振动的振幅--频率关系图象.由图可知,落在网上的昆虫翅膀振动的频率为200Hz左右时,蜘蛛感到网振动最为强烈,这种现象称为共振.
蜘蛛虽有8只眼睛,但视力很差,完全靠感觉来捕食和生活,它的腿能敏捷地感觉到丝网的振动,如图所示为丝网做受迫振动的振幅--频率关系图象.由图可知,落在网上的昆虫翅膀振动的频率为200Hz左右时,蜘蛛感到网振动最为强烈,这种现象称为共振.