题目内容
10. 如图竖直面内有一半径R=0.4m光滑半圆轨道,圆心在O点,BOD在同一竖直线上,圆弧在B点与水平传送带相切,水平传送带逆时针运动,速度大小为3m/s,AB长L=2m,将质量m=1kg的小滑块从A点由静止释放,滑块与皮带间动摩擦因数为0.4,g取10m/s2,下列说法正确的是( )
如图竖直面内有一半径R=0.4m光滑半圆轨道,圆心在O点,BOD在同一竖直线上,圆弧在B点与水平传送带相切,水平传送带逆时针运动,速度大小为3m/s,AB长L=2m,将质量m=1kg的小滑块从A点由静止释放,滑块与皮带间动摩擦因数为0.4,g取10m/s2,下列说法正确的是( )| A. | 滑块刚进入圆弧轨道时对轨道压力为10N | |
| B. | 滑块在C点对轨道的压力为2.5N | |
| C. | 若只减小滑块质量,滑块到达C点时速度不变 | |
| D. | 若传送带速度足够大,小滑块一定能通过D点 |
分析 根据受力分析求得滑块在传送带上的运动情况,进而得到在B点的速度,然后由牛顿第二定律求得支持力,即可由牛顿第三定律求得压力;再根据在半圆轨道上机械能守恒求得在C点的速度.
解答 解:A、滑块在传送带上运动,当速度小于传送带速度时,合外力为摩擦力μmg,故加速度a=μg=4m/s2;
那么,滑块要达到传送带速度需要运动时间$t=\frac{v}{a}=0.75s$,运动位移$s=\frac{{v}^{2}}{2a}=\frac{9}{8}m$;
所以,滑块到达B点前就达到传送带速度,然后匀速运动到B点;
所以,滑块刚进入圆弧轨道时的速度为3m/s,那么由牛顿第二定律可得:滑块刚进入圆弧轨道时受到的支持力${F}_{N}=mg+m\frac{{v}^{2}}{R}=32.5N$;
那么,由牛顿第三定律可知:滑块刚进入圆弧轨道时对轨道压力为32.5N,故A错误;
C、由A可知,滑块到达B点的速度为3m/s,与滑块质量无关;
滑块在半圆轨道上运动,只有重力做功,那么由机械能守恒可得:$\frac{1}{2}m{v}^{2}=mgR+\frac{1}{2}m{{v}_{C}}^{2}$,所以,vC=1m/s,与质量无关,故若只减小滑块质量,滑块到达C点时速度不变,故C正确;
B、滑块在C点时,轨道对滑块的支持力沿CO方向,滑块只受重力、支持力作用,故支持力做向心力,即${F}_{N}=\frac{m{{v}_{C}}^{2}}{R}=2.5N$,故由牛顿第三定律可得:滑块在C点对轨道的压力为2.5N,故B正确;
D、若传送带速度足够大,那么滑块的速度恒小于传送带速度,所以,滑块从A到B一直做加速运动,那么,滑块在B点的速度${v}_{B}=\sqrt{2aL}=4m/s$;
若滑块能通过D点,那么对滑块在D点应用牛顿第二定律可得:$mg≤\frac{m{{v}_{D}}^{2}}{R}$;
又有滑块从B到D只有重力做功,机械能守恒,所以由$\frac{1}{2}m{v}_{B}{′}^{2}=2mgR+\frac{1}{2}m{{v}_{D}}^{2}≥\frac{5}{2}mgR$,所以,${v}_{B}′≥\sqrt{5gR}=\sqrt{20}m/s>{v}_{B}$;所以,滑块肯定不能到达D点,故D错误;
故选:BC.
点评 物体运动学问题,一般先对物体进行受力分析,然后根据牛顿第二定律及动能定理求解状态量及做功问题,然后再根据运动学规律取得位移、运动时间等过程量.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案 如图为氢原子的能级示意图,锌的逸出功是3.34eV,那么对氢原子在能级跃迁过程中发射或吸收光子的规律认识错误的是( )
如图为氢原子的能级示意图,锌的逸出功是3.34eV,那么对氢原子在能级跃迁过程中发射或吸收光子的规律认识错误的是( )| A. | 用能量为14.0eV的光子照射,可使处于基态的氢原子电离 | |
| B. | 一群处于n=4能级的氢原子向低能级跃迁所辐射的光中,有3种不同频率的光能使锌发生光电效应 | |
| C. | 一群处于n=3能级的氢原子向基态跃迁时,发出的光照射锌板,锌板表面所发出的光电子的最大初动能为8.75eV | |
| D. | 用能量为10.21eV 的光子照射,可使处于基态的氢原子跃迁到激发态 |
| A. | 从今天看来,哥白尼提出的“日心说”是正确的 | |
| B. | 牛顿提出了万有引力定律 | |
| C. | 开普勒认为太阳系中各大行星的运动方向总是与它和太阳的连线垂直 | |
| D. | 第谷首先提出了地球绕太阳的运动轨道是椭圆轨道运动而不是圆轨道 |
 杂技演员骑独轮车走钢索示意图如下,钢索两端等高,间距为20m,杂技演员连同独轮车平衡杆总共70kg,当钢索长度约为35m,则钢索所能允许承受的最大拉力可能为( )
杂技演员骑独轮车走钢索示意图如下,钢索两端等高,间距为20m,杂技演员连同独轮车平衡杆总共70kg,当钢索长度约为35m,则钢索所能允许承受的最大拉力可能为( )| A. | 500N | B. | 2000N | C. | 8000N | D. | 600N |

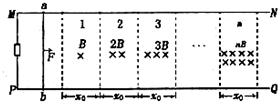 如图所示.两平行光滑的金属导轨MN、PQ固定在水平面上,相距为L,处于竖直向下的磁场中,整个磁场由n个宽度皆为x0的条形匀强磁场区域1、2…n组成,从左向右依次排列,磁感应强度的大小分别为B、2B、3B…nB,两导轨左端MP间接入电阻R,一质量为m的金属棒ab垂直于MN、PQ放在水平导轨上,与导轨电接触良好,不计导轨和金属棒的电阻.
如图所示.两平行光滑的金属导轨MN、PQ固定在水平面上,相距为L,处于竖直向下的磁场中,整个磁场由n个宽度皆为x0的条形匀强磁场区域1、2…n组成,从左向右依次排列,磁感应强度的大小分别为B、2B、3B…nB,两导轨左端MP间接入电阻R,一质量为m的金属棒ab垂直于MN、PQ放在水平导轨上,与导轨电接触良好,不计导轨和金属棒的电阻.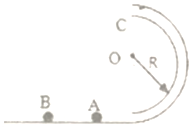 如图所示,半径R=0.2m,内径很小的光滑半圆管竖直固定放置,质量分别为m、2m的小球A和B(可看做质点)静止与光滑轨道的水平部分(小球的直径略小于半圆管的内径),现给小球一水平向右的初速度使其与小球A发生正碰,碰后A球通过最高点C时,对外管壁的压力大小为3mg,B球通过最高点C时,对内管壁的压力大小为mg,取g=10m/s2,求:
如图所示,半径R=0.2m,内径很小的光滑半圆管竖直固定放置,质量分别为m、2m的小球A和B(可看做质点)静止与光滑轨道的水平部分(小球的直径略小于半圆管的内径),现给小球一水平向右的初速度使其与小球A发生正碰,碰后A球通过最高点C时,对外管壁的压力大小为3mg,B球通过最高点C时,对内管壁的压力大小为mg,取g=10m/s2,求: