题目内容
11.无线充电的原理如图所示:通过插座上的电流转化器,将电能转化为超声波,用电设备上的接收器捕获超声波,再转化为电能给设备充电.接收器单位面积上接收到的超声波功率与接收器和电流转化器之间距离s的平方成反比,其将超声波转化为电能的转化效率为η1.某电动小车(含接收器)质量为 m,其电池将电能转为机械能的效率为η2.用该装置给其充电:当充电站到电流转换器的距离s=s0时,经过时间 t0小车刚好充满电.然后启动小车沿平直道路行驶,其所受阻力恒为0.2mg,经过10R的距离(电能已耗尽)后进入一个半径为 R 的竖直放置的光滑圆形轨道,在最高点时对轨道的压力大小恰为mg.小车离开充电站后会自动停止充电,己知重力加速度为 g.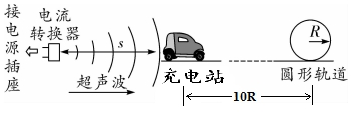
求:
(1)电动小车在轨道最高点的速度;
(2)当 s=s0时,小车接收器接收到的超声波功率 P0;
(3)若改变电流转换器与充电站间的距离 s,要使小车不脱离圆形轨道做完整圆周运动,充电时间 t 与距离 s 应满足什么关系?
分析 (1)电动小车在最高点受重力和支持力,合力提供向心力,根据向心力公式求出电动小车在轨道最高点的速度;
(2)根据机械能守恒定律和动能定理列式求出接收器接受到的超声波的功率P0;
(3)要使小车不脱离圆形轨道做完整的圆周运动,则小车能达到最高点,根据能量守恒定律和动能定理列式求解即可.
解答 解:(1)在最高点,由向心力公式得,mg+FN=m$\frac{{v}^{2}}{R}$,
又因为FN=mg,
由以上两式可解得:v=$\sqrt{2gR}$.
(2)设小车在水平轨道上的动能为Ek,
从水平轨道到最高点满足机械能守恒,
即:Ek=mg•2R+$\frac{1}{2}$mv2,
解得:Ek=3mgR,
由动能定理得,P0t0η1η2-0.2mg•10R=Ek,
解得:P0=$\frac{5mgR}{{η}_{1}{η}_{2}{t}_{0}}$.
(3)要使小车不脱离圆形轨道做完整的圆周运动,
若恰好达到轨道最高点,则有:mg=m $\frac{{v}_{1}^{2}}{R}$,
从水平轨道到最高点满足机械能守恒,
则有:Ek1=mg•2R+$\frac{1}{2}$m${v}_{1}^{2}$,
又因为Ek1=P1tη1η2-0.2mg•10R,
解得:P1=$\frac{4.5mgR}{{η}_{1}{η}_{2}t}$,
则有:$\frac{{P}_{0}}{{P}_{1}}$=$\frac{\frac{5mgR}{{η}_{1}{η}_{2}{t}_{0}}}{\frac{4.5mgR}{{η}_{1}{η}_{2}t}}$=$\frac{10t}{9{t}_{0}}$,
又因为$\frac{{P}_{0}}{P}$=$\frac{{s}^{2}}{{s}_{0}^{2}}$,
由以上两式可解得:t=$\frac{9{s}^{2}{t}_{0}}{10{s}_{0}^{2}}$
故能通过最高点的条件是:t≥$\frac{9{s}^{2}{t}_{0}}{10{s}_{0}^{2}}$.
答:(1)电动小车在轨道最高点的速度为$\sqrt{2gR}$;
(2)当 s=s0时,小车接收器接收到的超声波功率P0=$\frac{5mgR}{{η}_{1}{η}_{2}{t}_{0}}$;
(3)充电时间 t 与距离 s 应满足的关系是t≥$\frac{9{s}^{2}{t}_{0}}{10{s}_{0}^{2}}$.
点评 解答本题关键要明确小车的运动规律,结合机械能守恒定律、能量守恒定律、牛顿第二定律列式求解,注意恰好到达最高点的条件,难度适中.


| A. | 第1s内和第3s内的运动方向相反 | B. | 第3s内和第4s内的加速度不相同 | ||
| C. | 第1s内和第4s内的位移大小相等 | D. | 0~2s和0~4s内的平均速度大小相等 |
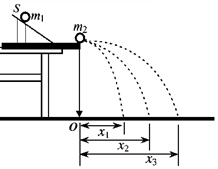 如图所示,用“碰撞实验器”可以验证动量守恒定律,即验证两个小球在水平轨道末端碰撞前后的动量守恒.入射小球质量为m1,被碰小球质量为m2,O点是小球抛出点在水平地面上的投影.实验时,先让入射小球m1多次从倾斜轨道上S位置静止释放,找到其平均落地点的位置,并记下此位置距O点的距离;然后把被碰小球m2静置于水平轨道末端,再将入射小球m1从倾斜轨道上S位置静止释放,与小球m2相撞,多次重复此过程,并分别找到它们平均落点的位置距O点的距离.则下列说法正确的是( )
如图所示,用“碰撞实验器”可以验证动量守恒定律,即验证两个小球在水平轨道末端碰撞前后的动量守恒.入射小球质量为m1,被碰小球质量为m2,O点是小球抛出点在水平地面上的投影.实验时,先让入射小球m1多次从倾斜轨道上S位置静止释放,找到其平均落地点的位置,并记下此位置距O点的距离;然后把被碰小球m2静置于水平轨道末端,再将入射小球m1从倾斜轨道上S位置静止释放,与小球m2相撞,多次重复此过程,并分别找到它们平均落点的位置距O点的距离.则下列说法正确的是( )| A. | 实验中要求两小球半径相等,且满足m1<m2 | |
| B. | 实验中要求倾斜轨道必须光滑 | |
| C. | 如果等式m1x2=m1x1+m2x3成立,可验证两小球碰撞过程动量守恒 | |
| D. | 如果等式m1x3=m1x1+m2x2成立,可验证两小球碰撞过程动量守恒 |
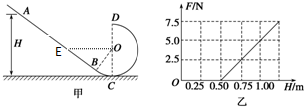
| A. | 圆轨道的半径为0.2m | |
| B. | 无法计算出小滑块的质量 | |
| C. | H取合适的值,可以使得小滑块经过最高点D后直接落到轨道AB上与圆心O等高的E点 | |
| D. | 由图乙可知,若H<0.50m,小滑块一定会在运动到D点之前脱离轨道 |
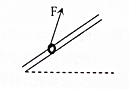 如图所示,一固定倾斜放置的粗糙长直杆,其上套有一质量为m的环,现对环施加一斜向上的力F后,下列说法正确的是( )
如图所示,一固定倾斜放置的粗糙长直杆,其上套有一质量为m的环,现对环施加一斜向上的力F后,下列说法正确的是( )| A. | 若环处于静止状态,则环所受摩擦力方向沿杆向上 | |
| B. | 若环处于静止状态,则力F越大,环所受摩擦力也越大 | |
| C. | 若环向上加速运动,则力F越大,环所受摩擦力也越大 | |
| D. | 若环向上匀速运动,则环所受摩擦力不可能为零 |
 如图所示,质量为m的小物块放在粗糙水平圆盘上,随圆盘一起然圆心O以角速度ω匀速转动,若物块与圆盘间的动摩擦因数为μ,物块到转轴的距离为R,重力加速度为g,则物块所受摩擦力( )
如图所示,质量为m的小物块放在粗糙水平圆盘上,随圆盘一起然圆心O以角速度ω匀速转动,若物块与圆盘间的动摩擦因数为μ,物块到转轴的距离为R,重力加速度为g,则物块所受摩擦力( )| A. | 大小一定等于mRω2 | B. | 大小一定等于μmg | ||
| C. | 方向指向圆心O | D. | 方向与物块运动的反向相反 |
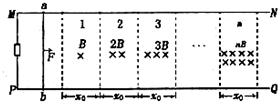 如图所示.两平行光滑的金属导轨MN、PQ固定在水平面上,相距为L,处于竖直向下的磁场中,整个磁场由n个宽度皆为x0的条形匀强磁场区域1、2…n组成,从左向右依次排列,磁感应强度的大小分别为B、2B、3B…nB,两导轨左端MP间接入电阻R,一质量为m的金属棒ab垂直于MN、PQ放在水平导轨上,与导轨电接触良好,不计导轨和金属棒的电阻.
如图所示.两平行光滑的金属导轨MN、PQ固定在水平面上,相距为L,处于竖直向下的磁场中,整个磁场由n个宽度皆为x0的条形匀强磁场区域1、2…n组成,从左向右依次排列,磁感应强度的大小分别为B、2B、3B…nB,两导轨左端MP间接入电阻R,一质量为m的金属棒ab垂直于MN、PQ放在水平导轨上,与导轨电接触良好,不计导轨和金属棒的电阻.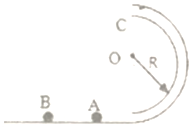 如图所示,半径R=0.2m,内径很小的光滑半圆管竖直固定放置,质量分别为m、2m的小球A和B(可看做质点)静止与光滑轨道的水平部分(小球的直径略小于半圆管的内径),现给小球一水平向右的初速度使其与小球A发生正碰,碰后A球通过最高点C时,对外管壁的压力大小为3mg,B球通过最高点C时,对内管壁的压力大小为mg,取g=10m/s2,求:
如图所示,半径R=0.2m,内径很小的光滑半圆管竖直固定放置,质量分别为m、2m的小球A和B(可看做质点)静止与光滑轨道的水平部分(小球的直径略小于半圆管的内径),现给小球一水平向右的初速度使其与小球A发生正碰,碰后A球通过最高点C时,对外管壁的压力大小为3mg,B球通过最高点C时,对内管壁的压力大小为mg,取g=10m/s2,求: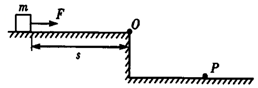 如图所示,水平桌面上距离桌面右端O点s=2m处有一个质量m=1kg、可看作质点的小滑块,小滑块从静止开始在5N的水平恒力作用下向右运动,过O点时撤去水平恒力,滑块落地点为P,已知P点到O点的水平距离为0.8m,到O点的竖直高度为0.2m.g取10m/s2,空气阻力不计.求:
如图所示,水平桌面上距离桌面右端O点s=2m处有一个质量m=1kg、可看作质点的小滑块,小滑块从静止开始在5N的水平恒力作用下向右运动,过O点时撤去水平恒力,滑块落地点为P,已知P点到O点的水平距离为0.8m,到O点的竖直高度为0.2m.g取10m/s2,空气阻力不计.求: