题目内容
18.据报道,我国将于2016年择机发射“天宫二号”,并计划于2020年发射“火星探测器”.设“天宫二号”绕地球做圆周运动的半径为r1、周期为T1;“火星探测器”绕火星做做圆周运动的半径为r2、周期为T2,万有引力常量为G.根据题设条件可得( )| A. | 关系式$\frac{{{r}_{1}}^{3}}{{{T}_{1}}^{2}}$=$\frac{{{r}_{2}}^{3}}{{{T}_{2}}^{2}}$ | |
| B. | 地球与火星的平均密度之比为$\frac{{{T}_{1}}^{2}}{{{T}_{2}}^{2}}$ | |
| C. | 地球与火星的质量之比为$\frac{{{r}_{1}}^{3}{{T}_{2}}^{2}}{{{r}_{2}}^{3}{{T}_{1}}^{2}}$ | |
| D. | “天宫二号”和“火星探测器”的向心加速度大小之比为$\frac{{r}_{1}{{T}_{2}}^{2}}{{r}_{2}{{T}_{1}}^{2}}$ |
分析 根据万有引力提供向心力列式,可求得地球和火星的质量.由于地球和火星本身的半径未知,是不能求出地球的密度的.根据圆周运动的向心加速度公式求向心加速度之比
解答 解:A、根据开普勒第三定律,“天宫二号”和“火星探测器”不是围绕同一个中心天体运动,所以有$\frac{{r}_{1}^{3}}{{T}_{1}^{2}}≠\frac{{r}_{2}^{3}}{{T}_{2}^{2}}$,故A错误;
B、因为地球和火星的半径不知道,所以无法算出地球和火星的体积,所以地球和火星的平均密度无法求,故B错误
C、根据万有引力提供向心力$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,得中心天体的质量为$M=\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{G{T}_{\;}^{2}}$,
“天宫二号”绕地球做圆周运动的半径为r1、周期为${T}_{1}^{\;}$,地球质量为${M}_{地}^{\;}=\frac{4{π}_{\;}^{2}{r}_{1}^{3}}{G{T}_{1}^{2}}$
“火星探测器”绕火星做做圆周运动的半径为r2、周期为${T}_{2}^{\;}$,火星质量为${M}_{火}^{\;}=\frac{4{π}_{\;}^{2}{r}_{2}^{3}}{G{T}_{2}^{2}}$
所以有$\frac{{M}_{地}^{\;}}{{M}_{火}^{\;}}=\frac{{r}_{1}^{3}{T}_{2}^{2}}{{r}_{2}^{3}{T}_{1}^{2}}$,故C正确;
D、根据圆周运动知识,向心加速度$a=\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$
“天宫二号”的向心加速度大小${a}_{1}^{\;}=\frac{4{π}_{\;}^{2}}{{T}_{1}^{2}}{r}_{1}^{\;}$
“火星探测器”的向心加速度大小${a}_{2}^{\;}=\frac{4{π}_{\;}^{2}}{{T}_{2}^{2}}{r}_{2}^{\;}$
“天宫二号”和“火星探测器”的向心加速度大小之比为$\frac{{a}_{1}^{\;}}{{a}_{2}^{\;}}=\frac{{r}_{1}^{\;}{T}_{2}^{2}}{{r}_{2}^{\;}{T}_{1}^{2}}$,故D正确
故选:CD
点评 解决本题的关键要明确卫星的运动模型,知道由万有引力提供其圆周运动向心力.本题也可以根据开普勒第三定律分析周期的大小.

 能考试全能100分系列答案
能考试全能100分系列答案| A. | 库仑利用扭秤实验测量出了万有引力常量G的大小 | |
| B. | 法拉第第一次发现电流的磁效应,并且制成了发电机 | |
| C. | 机械波在不同的介质中传播其频率不会发生改变 | |
| D. | 波长比障碍物尺寸小或相差不多时,会发生明显衍射现象 |
| A. | $\frac{gR{p}^{2}}{G{p}^{3}}$ | B. | $\frac{g{R}^{2}{q}^{3}}{G{p}^{2}}$ | C. | $\frac{gR{q}^{2}}{G{p}^{3}}$ | D. | $\frac{g{R}^{2}{p}^{3}}{G{q}^{2}}$ |
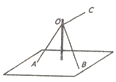 如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )| A. | 20$\sqrt{3}$N | B. | 40N | C. | 40$\sqrt{3}$N | D. | 60N |
 回旋加速器在核科学、核技术、核医学等高新技术领域得到了广泛应用,有力地推动了现代科学技术的发展.回旋加速器的原理如图所示,D1和D2是两个正对的中空半圆金属盒,它们的半径均为R,且分别接在电压一定的交流电源两端,可在两金属盒之间的狭缝处形成变化的加速电场,两金属盒处于与盒面垂直、磁感应强度为B的匀强磁场中,A点处的粒子源不断产生带电粒子,它们在两盒之间被电场加速后在金属盒内的磁场中做匀速圆周运动.调节交流电源的频率,使得每当带电粒子运动到现金金属盒之间的狭缝边缘时恰好改变加速电场的方向.从而保证带电粒子能在两金属盒之间狭缝处总被加速,且最终都能沿位于D2盒边缘的C口射出.该回旋加速器可将原来静止的α粒子(氦原子核)加速到最大速率v使它获得的最大动能为Ek.若带电粒子在A点的初速度、所受重力、通过狭缝的时间及C口的口径大小均可忽略不计,且不考虑相对论效应,则用该回旋加速器( )
回旋加速器在核科学、核技术、核医学等高新技术领域得到了广泛应用,有力地推动了现代科学技术的发展.回旋加速器的原理如图所示,D1和D2是两个正对的中空半圆金属盒,它们的半径均为R,且分别接在电压一定的交流电源两端,可在两金属盒之间的狭缝处形成变化的加速电场,两金属盒处于与盒面垂直、磁感应强度为B的匀强磁场中,A点处的粒子源不断产生带电粒子,它们在两盒之间被电场加速后在金属盒内的磁场中做匀速圆周运动.调节交流电源的频率,使得每当带电粒子运动到现金金属盒之间的狭缝边缘时恰好改变加速电场的方向.从而保证带电粒子能在两金属盒之间狭缝处总被加速,且最终都能沿位于D2盒边缘的C口射出.该回旋加速器可将原来静止的α粒子(氦原子核)加速到最大速率v使它获得的最大动能为Ek.若带电粒子在A点的初速度、所受重力、通过狭缝的时间及C口的口径大小均可忽略不计,且不考虑相对论效应,则用该回旋加速器( )| A. | 能使原来静止的质子获得的最大速率为$\frac{1}{2}$v | |
| B. | 能使原来静止的质子获得的动能为$\frac{1}{4}$Ek | |
| C. | 加速质子的交流电场频率与加速α粒子的交流电场频率之比为1:1 | |
| D. | 加速质子的总次数与加速α粒子总次数之比为2:1 |
| A. | $\frac{{v}_{A}}{{v}_{B}}=\frac{R}{R-d}\sqrt{\frac{R}{R+d}}$ | B. | $\frac{{v}_{A}}{{v}_{B}}=\frac{R}{R+d}\sqrt{\frac{R}{R-d}}$ | C. | $\frac{{v}_{A}}{{v}_{B}}=\frac{R+d}{R-d}$ | D. | $\frac{{v}_{A}}{{v}_{B}}=\sqrt{\frac{R-d}{R+d}}$ |
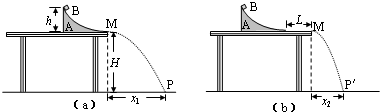
 如图所示,用力F把铁块压在竖直墙上,此时重力为G的物体沿墙壁匀速下滑,若物体与墙壁之间的动摩擦因数为μ,则物体所受摩擦力的大小等于μF或等于G.
如图所示,用力F把铁块压在竖直墙上,此时重力为G的物体沿墙壁匀速下滑,若物体与墙壁之间的动摩擦因数为μ,则物体所受摩擦力的大小等于μF或等于G.