题目内容
3.有一宇宙飞船,它的正面面积S=0.98m2,以v=2×103m/s的速度飞入一宇宙微粒尘区,此尘区每立方米空间有一个微粒,微粒的平均质量m=2×10-7kg,要使飞船速度保持不变,飞船的牵引力应增加多少?(设微粒与飞船外壳碰撞后附于飞船上).分析 选在时间△t内与飞船碰撞的微粒为研究对象,表示出其质量,再根据动量定理即可求解.
解答 解:选在时间△t内与飞船碰撞的微粒为研究对象,其质量应等于底面积为S,高为v△t的圆柱体内微粒的质量.
即 M=mSv△t,初动量为0,末动量为mv.
设飞船对微粒的作用力为F,由动量定理得:F•△t=Mv-0
则 F=$\frac{Mv}{△t}$=$\frac{mSv△t•v}{△t}$=mSv2;
根据牛顿第三定律可知,微粒对飞船的撞击力大小也等于mSv2,则飞船要保持原速度匀速飞行牵引力应增加F′=F=mSv2;
代入数据得:F′=2×10-4×10-3×0.98×(2×103)2N=0.78N
答:飞船的牵引力应增加0.78N
点评 本题主要考查了动量定理及根据牛顿第三定律的直接应用,关键要会选择研究对象,运用动量定理列式.

练习册系列答案
相关题目
13.甲、乙、丙三辆汽车在同一条平直公路上行驶.,先后以相同的速度通过同一个路标,从通过此路标开始.甲做匀速直线运动,乙做先做匀加速直线运动后做匀减速直线运动,丙做先做匀减速直线运动后做加速直线运动,它们到达下一个路标时的速度又相同,关于它们通过两个路标之间所用的时间长短,下列说法中正确的是( )
| A. | 甲用的时间最短 | B. | 乙用的时间最短 | ||
| C. | 丙用的时间最短 | D. | 它们用的时间相同. |
18.在水平面上有一个小物块质量为m,由0点从静止开始沿水平面做匀加速直线运动,经过A、B、C三点,A、B、C三点到0点距离分别为x1、x2、x3,由0点到A、B、C所用时间分别为t1、t2、t3,下列结论正确的是( )
| A. | $\frac{x_1}{{{t_1}^2}}=\frac{x_2}{{{t_2}^2}}=\frac{x_3}{{{t_3}^2}}$ | B. | $\frac{x_1}{t_1}<\frac{x_2}{t_2}<\frac{x_3}{t_3}$ | ||
| C. | $\frac{x_1}{t_1}=\frac{x_2}{t_2}=\frac{x_3}{t_3}$ | D. | $\frac{x_1}{{{t_1}^2}}<\frac{x_2}{{{t_2}^2}}<\frac{x_3}{{{t_3}^2}}$ |
8.两个等量同种点电荷,在其连接中点的场强和电势,以下说法中正确的是( )
| A. | 场强最大,电势为零 | B. | 场强为零,电势不为零 | ||
| C. | 场强不为零,电势也不为零 | D. | 场强为零,电势为零 |
8.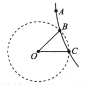 如图所示,在点O放置一个正点电荷,在过点O的竖直平面内的点A处自由释放一个带正电的小球,小球的质量为m,带电量为q.小球落下的轨迹如图中的实线所示,它与以点O为圆心,R为半径的圆(图中虚线所示)相交于B、C两点,点O、C在同一水平线上,∠BOC=30°,点A距OC的高度为h,若小球通过B点的速度为v,则( )
如图所示,在点O放置一个正点电荷,在过点O的竖直平面内的点A处自由释放一个带正电的小球,小球的质量为m,带电量为q.小球落下的轨迹如图中的实线所示,它与以点O为圆心,R为半径的圆(图中虚线所示)相交于B、C两点,点O、C在同一水平线上,∠BOC=30°,点A距OC的高度为h,若小球通过B点的速度为v,则( )
 如图所示,在点O放置一个正点电荷,在过点O的竖直平面内的点A处自由释放一个带正电的小球,小球的质量为m,带电量为q.小球落下的轨迹如图中的实线所示,它与以点O为圆心,R为半径的圆(图中虚线所示)相交于B、C两点,点O、C在同一水平线上,∠BOC=30°,点A距OC的高度为h,若小球通过B点的速度为v,则( )
如图所示,在点O放置一个正点电荷,在过点O的竖直平面内的点A处自由释放一个带正电的小球,小球的质量为m,带电量为q.小球落下的轨迹如图中的实线所示,它与以点O为圆心,R为半径的圆(图中虚线所示)相交于B、C两点,点O、C在同一水平线上,∠BOC=30°,点A距OC的高度为h,若小球通过B点的速度为v,则( )| A. | 小球运动到C点时的速度为$\sqrt{{v}^{2}+g(h-\frac{R}{2})}$ | |
| B. | 小球运动到C点的速度为$\sqrt{{v}^{2}+gR}$ | |
| C. | 小球从A点运动到C点的过程中电场力所做的功为$\frac{1}{2}$mv2-mg(h-$\frac{R}{2}$) | |
| D. | 小球从A点运动到C点的过程中电场力所做的功为$\frac{1}{2}$mv2-mgh |
9. 如图所示,两个固定的相同细环相距一定的距离,同轴放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷.一带正电的粒子从很远处沿轴线飞来并穿过两环.则在带电粒子运动过程中( )
如图所示,两个固定的相同细环相距一定的距离,同轴放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷.一带正电的粒子从很远处沿轴线飞来并穿过两环.则在带电粒子运动过程中( )
 如图所示,两个固定的相同细环相距一定的距离,同轴放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷.一带正电的粒子从很远处沿轴线飞来并穿过两环.则在带电粒子运动过程中( )
如图所示,两个固定的相同细环相距一定的距离,同轴放置,O1、O2分别为两环的圆心,两环分别带有均匀分布的等量异种电荷.一带正电的粒子从很远处沿轴线飞来并穿过两环.则在带电粒子运动过程中( )| A. | 在O1点粒子加速度方向向右 | |
| B. | 从O1到O2过程粒子电势能一直增加 | |
| C. | 轴线上O1点右侧存在一点,粒子在该点动能最小 | |
| D. | 轴线上O1点右侧,O2点左侧都存在场强为零的点,它们关于O1、O2连线中点对称 |
 请完成下列判断(判断语句如下:“不变”、“增大”或“减少”,“有”或“无”,或判断方向:从左向右或从右向左等),并将正确答案直接填写在横线上或空格处:
请完成下列判断(判断语句如下:“不变”、“增大”或“减少”,“有”或“无”,或判断方向:从左向右或从右向左等),并将正确答案直接填写在横线上或空格处:
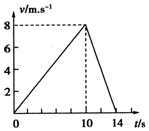 一物体由静止开始运动的速度-时间关系图象如图,求:
一物体由静止开始运动的速度-时间关系图象如图,求: