题目内容
20．
物体P放在粗糙水平地面上，劲度系数k=300N/m的轻弹簧左端固定在竖直墙壁上，右端固定在质量为m=1kg的物体P上，弹簧水平，如图所示．开始t=0时弹簧为原长，P从此刻开始受到与地面成θ=37°的拉力F作用而向右做加速度a=1m/s2的匀加速运动，某时刻t=t0时F=10N，弹簧弹力FT=6N，取sin37°=0.6、cos37°=0.8，重力加速度g=10m/s2．求：（1）t=t0时P的速度；
（2）物体与地面间的动摩擦因数μ．
分析 （1）根据胡克定律列式求解位移，根据速度位移公式列式求解初速度；
（2）t=t0时，对球受力分析，根据牛顿第二定律列式求解物体与地面间的动摩擦因数μ；
解答 解：（1）设t=t0时，弹簧伸长量为x，此时物体P的速度为v；
由胡克定律得：FT=kx …①
由匀变速直线运动规律有：v2=2ax …②
联立①②代入数据解得：v=0.2m/s．
（2）物体P所受的摩擦力：Ff=μ（mg-Fsin37°） …③
当t=t0时，由牛顿第二定律得：Fcos37°-FT-Ff=ma …④
联立③④解得：μ=0.25．
答：（1）t=t0时P的速度为0.2m/s；
（2）物体与地面间的动摩擦因数μ为0.25．
点评 本题是已知运动情况确定受力情况的问题，关键是先根据运动情况确定加速度，然后受力分析后根据牛顿第二定律并结合胡克定律列式分析，难度不大．
练习册系列答案
相关题目
11．
一列简谐横波在t=0时刻的波形如图中的实线所示，t=0.02s时刻的波形如图中虚线所示，则下列说法正确的是 （ ）
一列简谐横波在t=0时刻的波形如图中的实线所示，t=0.02s时刻的波形如图中虚线所示，则下列说法正确的是 （ ）| A． | 如果波向右传播，波速一定为1m/s | |
| B． | 如果波向右传播，波速可能为5m/s | |
| C． | 如果波向左传播，最小波速为3m/s | |
| D． | 如果波向左传播，波速一定是3m/s的整数倍 |
物体A的质量M=1kg，静止在光滑水平面上的平板车B的质量为m=0.5kg、长L=1m．某时刻A以V0=4m/s向右的初速度滑上木板B的上表面，在A滑上B的同时，给B施加一个水平向右的拉力．忽略物体A的大小，已知A与B之间的动摩擦因数?=0.2，取重力加速度g=10m/s2．试求：
5．
如图所示，人在岸上拉船，已知船的质量为m，水的阻力恒为f，当轻绳与水平面的夹角为θ时，船的速度为v，此时人的拉力大小为F，则（ ）
如图所示，人在岸上拉船，已知船的质量为m，水的阻力恒为f，当轻绳与水平面的夹角为θ时，船的速度为v，此时人的拉力大小为F，则（ ）| A． | 人拉绳行走的速度为vsinθ | B． | 人拉绳行走的速度为$\frac{v}{cosθ}$ | ||
| C． | 船的加速度为 $\frac{Fcosθ-f}{m}$ | D． | 船的加速度为 $\frac{F-f}{m}$ |
12．
如图所示，一固定杆与水平方向夹角为θ，将一个滑块套在杆上，一根轻绳一端系着滑块另一端悬挂小球，滑块与杆之间的摩擦不可忽略．当小球与滑块以相同的加速度一起运动时，绳与竖直方向的夹角为β，且β＞θ，则（ ）
如图所示，一固定杆与水平方向夹角为θ，将一个滑块套在杆上，一根轻绳一端系着滑块另一端悬挂小球，滑块与杆之间的摩擦不可忽略．当小球与滑块以相同的加速度一起运动时，绳与竖直方向的夹角为β，且β＞θ，则（ ）| A． | 滑块沿杆加速上滑 | B． | 滑块沿杆加速下滑 | ||
| C． | 滑块沿杆减速上滑 | D． | 滑块沿杆减速下滑 |
9．
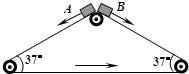如图所示，三角形传送带以1m/s的速度逆时针匀速转动，两边的传送带长都是2m，且与水平方向的夹角均为37°．现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑，两物块与传送带的动摩擦因数都是0.5，g=10m/s2，sin37°=0.6，cos37°=0.8．下列判断不正确的是（ ）
如图所示，三角形传送带以1m/s的速度逆时针匀速转动，两边的传送带长都是2m，且与水平方向的夹角均为37°．现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑，两物块与传送带的动摩擦因数都是0.5，g=10m/s2，sin37°=0.6，cos37°=0.8．下列判断不正确的是（ ）| A． | 物块A先到达传送带底端 | |
| B． | 物块AB同时到达传送带底端 | |
| C． | 传送带对物块AB的摩擦力都沿传送带向上 | |
| D． | 物块A下滑过程中相对传送带的位移小于物块B下滑过程中相对传送带的位移 |