题目内容
18．一装满水的开口玻璃杯用一细绳系住在竖直面内做圆周运动，当运动到圆周最高点时线速度为2m/s，为了使水不从杯口流出，杯子作圆周运动的半径不得超过多少米？分析 考虑临界情况，抓住杯底对水的弹力为零，根据重力提供向心力求出最大半径．
解答 解：在最高点，半径最大时，重力提供向心力，故：
mg=m$\frac{{v}^{2}}{r}$
解得：
r=$\frac{{v}^{2}}{g}$=$\frac{{2}^{2}}{10}m=0.4m$
答：杯子作圆周运动的半径不得超过0.4米．
点评 解决本题的关键掌握圆周运动向心力的来源，结合牛顿第二定律进行求解，掌握在最高点的临界情况．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
8．已知引力常量为G，地球半径为R，地球表面重力加速度为g，近地卫星绕地球转动的周期为T，地球的第一宇宙速度为v，则地球的平均密度可表示为（ ）
| A． | $ρ=\frac{3π}{{G{T^2}}}$ | B． | $ρ=\frac{{3{v^2}}}{4πRG}$ | C． | $ρ=\frac{3g}{4πRG}$ | D． | $ρ=\frac{{3{v^2}}}{{4π{R^2}G}}$ |
9．A、B两个质点，分别做匀速圆周运动，在相等时间内它们通过的弧长比SA：SB=2：3，转过的圆心角比θA：θB=3：2．则下列说法中正确的是（ ）
| A． | 它们的线速度比vA：vB=1：1 | B． | 它们的向心加速度比2：3 | ||
| C． | 它们的周期比TA：TB=2：3 | D． | 它们的周期比TA：TB=1：2 |
如图是宇航员在地面上空进行“太空行走”的情景，当他出舱后相对飞船静止不动时，他处于失重（选填超重、失重、平衡）状态；现已知地球的半径R和引力常数G，若想要根据万有引力提供飞船做圆周运动的向心力来计算地球的质量，还需要知道该飞船的哪些运动信息：周期T、与地面的高度h（写出相关物理量及对应的物理符号）．
如图，一个质量为0.6kg的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧．已知圆弧的半径R=0.3m，θ=60°，小球到达A点时的速度VA=4m/s．（取g=10m/s2）求：
3．
A、B两个物体的质量分别为m1和m2，并排静止在水平地面上，用同向水平拉力F1、F2分别作用于物体A和B上，作用一段时间后撤去，两物体各自滑行一段距离后停止下来，两物体运动的速度-时间图象分别如图中图线a、b所示，已知拉力F1、F2分别撤去后，物体做减速运动过程的速度-时间图线彼此平行（相关数据已在图中标出），由图中信息可以得出（ ）
A、B两个物体的质量分别为m1和m2，并排静止在水平地面上，用同向水平拉力F1、F2分别作用于物体A和B上，作用一段时间后撤去，两物体各自滑行一段距离后停止下来，两物体运动的速度-时间图象分别如图中图线a、b所示，已知拉力F1、F2分别撤去后，物体做减速运动过程的速度-时间图线彼此平行（相关数据已在图中标出），由图中信息可以得出（ ）| A． | 若F1=F2，则m1＜m2 | |
| B． | 若m1=m2，则力F1对物体A所做的功较多 | |
| C． | 若m1=m2，则整个过程中摩擦力对B物体做的功较多 | |
| D． | 若m1=m2，则整个过程中摩擦力对A和B物体做的功一样多 |
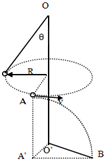如图所示，竖直刚性杆OO′固定在水平地面上，轻质细绳一端悬于O点，另一端连接一质量为m的小球（可视为质点），小球绕竖直轴OO′在某一水平面上做匀速圆周运动，细绳到轴OO′的垂直距离为R=0.1m，细绳与竖直轴OO′的夹角为θ=45°；当小球经过A点时，细绳在A点被烧断，A距地面的高度为h=1.2m（A′是A点在水平面上的投影），小球落地点为B，取g=10m/s2．求：
8．
如图所示，在A，B两点固定等量正点电荷，C是两点电荷连线上靠近A的一点．在C点处由静止释放一带正电的试探电荷q，电荷q仅在电场力的作用下向右运动的过程中，先后经过P，Q两点（图中未画出），则（ ）
如图所示，在A，B两点固定等量正点电荷，C是两点电荷连线上靠近A的一点．在C点处由静止释放一带正电的试探电荷q，电荷q仅在电场力的作用下向右运动的过程中，先后经过P，Q两点（图中未画出），则（ ）| A． | 电荷q在P点的电势能一定大于在Q点的电势能 | |
| B． | 电荷q在P点的电势能可能等于在Q点的电势能 | |
| C． | 电荷q在C点的电势能一定小于在P点的电势能 | |
| D． | 电荷q在C点的电势能一定不小于在Q点的电势能 |