题目内容
10.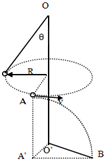 如图所示,竖直刚性杆OO′固定在水平地面上,轻质细绳一端悬于O点,另一端连接一质量为m的小球(可视为质点),小球绕竖直轴OO′在某一水平面上做匀速圆周运动,细绳到轴OO′的垂直距离为R=0.1m,细绳与竖直轴OO′的夹角为θ=45°;当小球经过A点时,细绳在A点被烧断,A距地面的高度为h=1.2m(A′是A点在水平面上的投影),小球落地点为B,取g=10m/s2.求:
如图所示,竖直刚性杆OO′固定在水平地面上,轻质细绳一端悬于O点,另一端连接一质量为m的小球(可视为质点),小球绕竖直轴OO′在某一水平面上做匀速圆周运动,细绳到轴OO′的垂直距离为R=0.1m,细绳与竖直轴OO′的夹角为θ=45°;当小球经过A点时,细绳在A点被烧断,A距地面的高度为h=1.2m(A′是A点在水平面上的投影),小球落地点为B,取g=10m/s2.求:(1)小球运动到A点时的速度大小;
(2)B点距竖直轴OO′的水平距离(即O′B的长度).
分析 (1)小球做匀速圆周运动,合外力提供向心力,对小球受力分析,根据向心力公式求解速度;
(2)细绳在A点被烧断,小球做平抛运动,根据平抛运动的基本公式结合几何关系求解.
解答 解:(1)对小球受力分析,受到重力和绳子的拉力,合力提供向心力,则有:
mgtan45°=m$\frac{{v}^{2}}{R}$
解得:v=$\sqrt{gR}=1m/s$
(2)细绳在A点被烧断,小球做平抛运动,运动的时间t=$\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×1.2}{10}}=\sqrt{0.24}s$,
则运动的水平位移x=vt=$\sqrt{0.24}m$,
根据几何关系可知,O′B的长度s=$\sqrt{{x}^{2}+{R}^{2}}=\sqrt{0.25}=0.5m$
答:(1)小球运动到A点时的速度大小为1m/;
(2)B点距竖直轴OO′的水平距离为0.5m
点评 本题主要考查了向心力公式以及平抛运动基本公式的直接应用,要求同学们能正确对小球进行受力分析,知道细绳在A点被烧断,小球做平抛运动,难度不大,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20. 如图所示,小球自a点由静止自由下落,到b点与竖直放置的轻弹簧接触,到c点时弹簧被压缩到最短,不计空气阻力,则小球在a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点与竖直放置的轻弹簧接触,到c点时弹簧被压缩到最短,不计空气阻力,则小球在a→b→c的运动过程中( )
 如图所示,小球自a点由静止自由下落,到b点与竖直放置的轻弹簧接触,到c点时弹簧被压缩到最短,不计空气阻力,则小球在a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点与竖直放置的轻弹簧接触,到c点时弹簧被压缩到最短,不计空气阻力,则小球在a→b→c的运动过程中( )| A. | 小球的加速度在ab段不变,在bc段逐渐变小 | |
| B. | 小球的速度在bc段逐渐减小 | |
| C. | 小球的重力势能在a→b→c过程中不断减小 | |
| D. | 弹簧的弹性势能在bc段先增大后减小 |
5. 如图所示,小球能在竖直放置的光滑圆形管道内做完整圆周运动,内侧壁半径为R(小球的直径略小于管道横截面的直径),小球可视为质点,则下列说法正确的是( )
如图所示,小球能在竖直放置的光滑圆形管道内做完整圆周运动,内侧壁半径为R(小球的直径略小于管道横截面的直径),小球可视为质点,则下列说法正确的是( )
 如图所示,小球能在竖直放置的光滑圆形管道内做完整圆周运动,内侧壁半径为R(小球的直径略小于管道横截面的直径),小球可视为质点,则下列说法正确的是( )
如图所示,小球能在竖直放置的光滑圆形管道内做完整圆周运动,内侧壁半径为R(小球的直径略小于管道横截面的直径),小球可视为质点,则下列说法正确的是( )| A. | 小球在最高点的最小速度为$\sqrt{gR}$ | |
| B. | 小球在最低点的最小速度为$\sqrt{5gR}$ | |
| C. | 小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力 | |
| D. | 小球在水平线ab以下的管道中运动时,内侧管壁对小球一定无作用力 |
15. 某同学在网球训练中,网球在不同高度A、B处与竖直墙壁碰撞后,垂直墙面弹出,均落在水平地面上的C处,如图所示.若网球弹出时速度大小分别为vA、vB,从弹出到落地的时间分别为tA、tB,则( )
某同学在网球训练中,网球在不同高度A、B处与竖直墙壁碰撞后,垂直墙面弹出,均落在水平地面上的C处,如图所示.若网球弹出时速度大小分别为vA、vB,从弹出到落地的时间分别为tA、tB,则( )
 某同学在网球训练中,网球在不同高度A、B处与竖直墙壁碰撞后,垂直墙面弹出,均落在水平地面上的C处,如图所示.若网球弹出时速度大小分别为vA、vB,从弹出到落地的时间分别为tA、tB,则( )
某同学在网球训练中,网球在不同高度A、B处与竖直墙壁碰撞后,垂直墙面弹出,均落在水平地面上的C处,如图所示.若网球弹出时速度大小分别为vA、vB,从弹出到落地的时间分别为tA、tB,则( )| A. | tA=tB | B. | tA<tB | C. | vA=vB | D. | vA<vB |
19. 在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
 在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )| A. | 顺时针 转速n=$\frac{v}{2πL}$ | B. | 顺时针 转速n=$\frac{v}{L}$ | ||
| C. | 逆时针 转速n=$\frac{v}{2πL}$ | D. | 逆时针 转速n=$\frac{v}{L}$ |
20.健身球是一个充满气体的大皮球,当人压向健身球上时,假设球内气体温度不变,则在这个过程中( )


| A. | 气体分子的平均动能增大 | B. | 气体的密度增大 | ||
| C. | 气体从外界吸收热量 | D. | 外界对气体做功 |
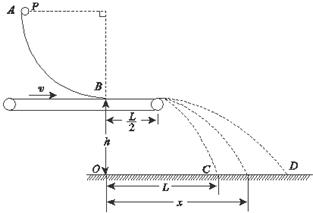 如图所示,AB是固定于竖直平面内的$\frac{1}{4}$圆弧形光滑轨道,末端B处的切线方向水平.一物体(可视为质点)P从圆弧最高点A处由静止释放,滑到B端飞出,落到地面上的C点.测得C点和B点的水平距离OC=L,B点距地面的高度OB=h.现在轨道下方紧贴B端安装一个水平传送带,传送带的右端与B点的距离为$\frac{L}{2}$.当传送带静止时,让物体P从A处由静止释放,物体P沿轨道滑过B点后又在传送带上滑行并从传送带的右端水平飞出,仍然落到地面上的C点.求:
如图所示,AB是固定于竖直平面内的$\frac{1}{4}$圆弧形光滑轨道,末端B处的切线方向水平.一物体(可视为质点)P从圆弧最高点A处由静止释放,滑到B端飞出,落到地面上的C点.测得C点和B点的水平距离OC=L,B点距地面的高度OB=h.现在轨道下方紧贴B端安装一个水平传送带,传送带的右端与B点的距离为$\frac{L}{2}$.当传送带静止时,让物体P从A处由静止释放,物体P沿轨道滑过B点后又在传送带上滑行并从传送带的右端水平飞出,仍然落到地面上的C点.求: 如图所示,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,va:vc=1:1,ωa:ωb=2:1.
如图所示,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,va:vc=1:1,ωa:ωb=2:1.