题目内容
13. 如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧.已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度VA=4m/s.(取g=10m/s2)求:
如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧.已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度VA=4m/s.(取g=10m/s2)求:(1)小球做平抛运动的初速度v0;
(2)P点与A点的水平距离和竖直高度;
(3)小球到达圆弧最高点C时vC=$\sqrt{7}$m/s,求对轨道的压力.
分析 (1)恰好从光滑圆弧ABC的A点的切线方向进入圆弧,说明到到A点的速度vA方向与水平方向的夹角为θ,这样可以求出初速度v0;
(2)平抛运动水平方向做匀速直线运动,竖直方向做自由落体运动,根据平抛运动的基本规律求出P点与A点的水平距离和竖直距离;
(3)在C点,重力和弹力的合力提供向心力,根据向心力公式和牛顿第二定律列式求出小球在最高点C时对轨道的压力.
解答 解:(1)小球到A点的速度如图所示,由图可知
v0=vx=vAcosθ=4×cos60°=2m/s
(2)根据平抛运动的分运动公式,有:
${v}_{y}={v}_{A}sinθ=4×sin60°=2\sqrt{3}m/s$
由平抛运动规律得:
${v}_{y}^{2}=2gh$
vy=gt
x=v0t
h=0.6m
x=0.4$\sqrt{3}$m≈0.69m
(3)由圆周运动向心力公式得:
${N}_{C}+mg=m\frac{{v}_{C}^{2}}{R}$
代入数据得:
NC=8N
由牛顿第三定律得:小球对轨道的压力大小:
NC′=NC=8N,方向竖直向上
答:(1)小球做平抛运动的初速度v0为2m/s;
(2)P点与A点的水平距离为0.69m,竖直高度为0.6m;
(3)小球到达圆弧最高点C时vC=$\sqrt{7}$m/s,对轨道的压力为8N.
点评 本题是平抛运动和圆周运动相结合的典型题目,除了运用平抛运动和圆周运动的基本公式外;本题第三问中C点速度可以利用动能定理求解出来.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
4.一列简谐波某时刻的波形如图中实线所示.经过0.5s后的波形如图中的虚线所示.已知波的周期为T,且0.25s<T<0.5s,则( )


| A. | 不论波向x轴哪一方向传播,在这0.5s内,x=1m处的质点M通过的路程都相等 | |
| B. | 当波向+x方向传播时,波速等于10m/s | |
| C. | 当波沿+x方向传播时,x=1m处的质点M和x=2.5m处的质点N在这0.5s内通过的路程相等 | |
| D. | 当波沿-x方向传播时,经过0.1s时,质点M的位移一定为零 |
8.一个从地面竖直上抛的物体,它两次经过一个较低点a的时间间隔为Ta,两次经过一个较高点b的时间间隔为Tb,则a、b之间的距离为( )
| A. | $\frac{1}{8}$g(Ta2-Tb2) | B. | $\frac{1}{4}$g(Ta2-Tb2) | C. | $\frac{1}{2}$g(Ta2-Tb2) | D. | $\frac{1}{2}$g(Ta2+Tb2) |
5. 如图所示,小球能在竖直放置的光滑圆形管道内做完整圆周运动,内侧壁半径为R(小球的直径略小于管道横截面的直径),小球可视为质点,则下列说法正确的是( )
如图所示,小球能在竖直放置的光滑圆形管道内做完整圆周运动,内侧壁半径为R(小球的直径略小于管道横截面的直径),小球可视为质点,则下列说法正确的是( )
 如图所示,小球能在竖直放置的光滑圆形管道内做完整圆周运动,内侧壁半径为R(小球的直径略小于管道横截面的直径),小球可视为质点,则下列说法正确的是( )
如图所示,小球能在竖直放置的光滑圆形管道内做完整圆周运动,内侧壁半径为R(小球的直径略小于管道横截面的直径),小球可视为质点,则下列说法正确的是( )| A. | 小球在最高点的最小速度为$\sqrt{gR}$ | |
| B. | 小球在最低点的最小速度为$\sqrt{5gR}$ | |
| C. | 小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力 | |
| D. | 小球在水平线ab以下的管道中运动时,内侧管壁对小球一定无作用力 |
3. 如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
 如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )
如图所示,质量为m1,长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间的滑动摩擦力的大小为f,用水平的恒定拉力F作用于滑块,当滑块从静止开始运动到木板右端时,木板在地面上移动的距离为s,滑块速度为v1,木板速度为v2,下列结论中正确的是( )| A. | 滑块克服摩擦力所做的功为fL | |
| B. | 上述过程满足(F-f)(L+s)=$\frac{1}{2}$mv12+$\frac{1}{2}{m}_{1}{{v}_{2}}^{2}$ | |
| C. | 其他条件不变的情况下,F越大,滑块到达右端所用时间越长 | |
| D. | 其他条件不变的情况下,f越大,滑块与木板间产生的热量越多 |

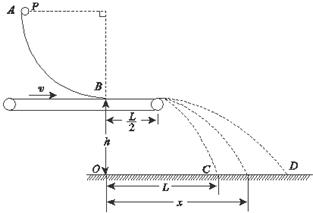 如图所示,AB是固定于竖直平面内的$\frac{1}{4}$圆弧形光滑轨道,末端B处的切线方向水平.一物体(可视为质点)P从圆弧最高点A处由静止释放,滑到B端飞出,落到地面上的C点.测得C点和B点的水平距离OC=L,B点距地面的高度OB=h.现在轨道下方紧贴B端安装一个水平传送带,传送带的右端与B点的距离为$\frac{L}{2}$.当传送带静止时,让物体P从A处由静止释放,物体P沿轨道滑过B点后又在传送带上滑行并从传送带的右端水平飞出,仍然落到地面上的C点.求:
如图所示,AB是固定于竖直平面内的$\frac{1}{4}$圆弧形光滑轨道,末端B处的切线方向水平.一物体(可视为质点)P从圆弧最高点A处由静止释放,滑到B端飞出,落到地面上的C点.测得C点和B点的水平距离OC=L,B点距地面的高度OB=h.现在轨道下方紧贴B端安装一个水平传送带,传送带的右端与B点的距离为$\frac{L}{2}$.当传送带静止时,让物体P从A处由静止释放,物体P沿轨道滑过B点后又在传送带上滑行并从传送带的右端水平飞出,仍然落到地面上的C点.求: 如图所示,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,va:vc=1:1,ωa:ωb=2:1.
如图所示,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,va:vc=1:1,ωa:ωb=2:1.