题目内容
9.A、B两个质点,分别做匀速圆周运动,在相等时间内它们通过的弧长比SA:SB=2:3,转过的圆心角比θA:θB=3:2.则下列说法中正确的是( )| A. | 它们的线速度比vA:vB=1:1 | B. | 它们的向心加速度比2:3 | ||
| C. | 它们的周期比TA:TB=2:3 | D. | 它们的周期比TA:TB=1:2 |
分析 根据公式v=$\frac{s}{t}$求解线速度之比,根据公式ω=$\frac{θ}{t}$求解角速度之比,根据a=vω知向心加速度比;根据公式T=$\frac{2π}{ω}$求周期之比.
解答 解:A、B两质点分别做匀速圆周运动,若在相等时间内它们通过的弧长之比为SA:SB=2:3,根据公式公式v=$\frac{s}{t}$,线速度之比为vA:vB=2:3,故A错误;
B、通过的圆心角之比φA:φB=3:2,根据公式ω=式ω=$\frac{θ}{t}$,角速度之比为3:2,根据a=vω
知向心加速度比:(2×3):(3×2)=1:1,故B错误;
C、根据公式T=$\frac{2π}{ω}$,周期之比为TA:TB=2:3,故C正确,D错误;
故选:C
点评 本题关键是记住线速度、角速度、周期和向心加速度的公式,根据公式列式分析,基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
19.有一宇宙飞船到了某行星上(该行星没有自转运动),以速度v接近行星赤道表面匀速飞行,测出运动的周期为T,已知引力常量为G,则可得( )
| A. | 该行星的半径为$\frac{vT}{2π}$ | B. | 该行星的平均密度为$\frac{3π}{G{T}^{2}}$ | ||
| C. | 无法测出该行星的质量 | D. | 该行星表面的重力加速度为$\frac{2πv}{GT}$ |
20. 如图所示,小球自a点由静止自由下落,到b点与竖直放置的轻弹簧接触,到c点时弹簧被压缩到最短,不计空气阻力,则小球在a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点与竖直放置的轻弹簧接触,到c点时弹簧被压缩到最短,不计空气阻力,则小球在a→b→c的运动过程中( )
 如图所示,小球自a点由静止自由下落,到b点与竖直放置的轻弹簧接触,到c点时弹簧被压缩到最短,不计空气阻力,则小球在a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点与竖直放置的轻弹簧接触,到c点时弹簧被压缩到最短,不计空气阻力,则小球在a→b→c的运动过程中( )| A. | 小球的加速度在ab段不变,在bc段逐渐变小 | |
| B. | 小球的速度在bc段逐渐减小 | |
| C. | 小球的重力势能在a→b→c过程中不断减小 | |
| D. | 弹簧的弹性势能在bc段先增大后减小 |
4.一列简谐波某时刻的波形如图中实线所示.经过0.5s后的波形如图中的虚线所示.已知波的周期为T,且0.25s<T<0.5s,则( )


| A. | 不论波向x轴哪一方向传播,在这0.5s内,x=1m处的质点M通过的路程都相等 | |
| B. | 当波向+x方向传播时,波速等于10m/s | |
| C. | 当波沿+x方向传播时,x=1m处的质点M和x=2.5m处的质点N在这0.5s内通过的路程相等 | |
| D. | 当波沿-x方向传播时,经过0.1s时,质点M的位移一定为零 |
19. 在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
 在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )
在街头的理发店门口,常可以看到这样的标志:一个转动的圆筒,外表有彩色螺旋斜条纹,我们感觉条纹在沿竖直方向运动,但实际上条纹在竖直方向并没有升降,这是由于圆筒的转动而使我们的眼睛产生的错觉,如图所示,假设圆筒上的条纹是围绕圆筒的一条宽带,相邻两圈条纹在沿圆筒轴线方向的距离(即螺距)为L,如果我们观察到条纹以速度v向上运动,则圆筒的转动情况是(从上往下看)( )| A. | 顺时针 转速n=$\frac{v}{2πL}$ | B. | 顺时针 转速n=$\frac{v}{L}$ | ||
| C. | 逆时针 转速n=$\frac{v}{2πL}$ | D. | 逆时针 转速n=$\frac{v}{L}$ |

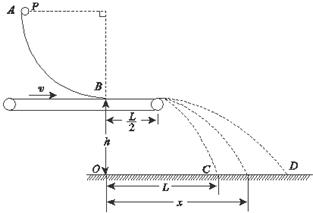 如图所示,AB是固定于竖直平面内的$\frac{1}{4}$圆弧形光滑轨道,末端B处的切线方向水平.一物体(可视为质点)P从圆弧最高点A处由静止释放,滑到B端飞出,落到地面上的C点.测得C点和B点的水平距离OC=L,B点距地面的高度OB=h.现在轨道下方紧贴B端安装一个水平传送带,传送带的右端与B点的距离为$\frac{L}{2}$.当传送带静止时,让物体P从A处由静止释放,物体P沿轨道滑过B点后又在传送带上滑行并从传送带的右端水平飞出,仍然落到地面上的C点.求:
如图所示,AB是固定于竖直平面内的$\frac{1}{4}$圆弧形光滑轨道,末端B处的切线方向水平.一物体(可视为质点)P从圆弧最高点A处由静止释放,滑到B端飞出,落到地面上的C点.测得C点和B点的水平距离OC=L,B点距地面的高度OB=h.现在轨道下方紧贴B端安装一个水平传送带,传送带的右端与B点的距离为$\frac{L}{2}$.当传送带静止时,让物体P从A处由静止释放,物体P沿轨道滑过B点后又在传送带上滑行并从传送带的右端水平飞出,仍然落到地面上的C点.求: