题目内容
17. 如图所示,质量为m的物体沿倾角为θ,长为l的固定光滑斜面从顶端由静止下滑到底端,则在此过程中重力做的功为mglsinθ,重力的平均功率为$mgsinθ\sqrt{\frac{glsinθ}{2}}$,滑到底端时重力的瞬时功率为$mgsinθ\sqrt{2glsinθ}$,支持力做功的功率为0.合外力做的功为mglsinθ.
如图所示,质量为m的物体沿倾角为θ,长为l的固定光滑斜面从顶端由静止下滑到底端,则在此过程中重力做的功为mglsinθ,重力的平均功率为$mgsinθ\sqrt{\frac{glsinθ}{2}}$,滑到底端时重力的瞬时功率为$mgsinθ\sqrt{2glsinθ}$,支持力做功的功率为0.合外力做的功为mglsinθ.
分析 根据下降的高度求出重力做功的大小,根据牛顿第二定律和运动学公式求出运动的时间和到达底端的速度,结合平均功率和瞬时功率公式分别求出平均功率和瞬时功率的大小.根据合力做功等于各力做功的代数和求出合力做功的大小.
解答 解:该过程中重力做功W=mgh=mglsinθ,
物体下滑的加速度a=gsinθ,根据l=$\frac{1}{2}a{t}^{2}$得运动的时间为:t=$\sqrt{\frac{2l}{a}}=\sqrt{\frac{2l}{gsinθ}}$,
重力的平均功率为:$\overline{P}=\frac{W}{t}$=$mglsinθ\sqrt{\frac{gsinθ}{2l}}$=$mgsinθ\sqrt{\frac{glsinθ}{2}}$.
物体滑动底端的速度为:$v=\sqrt{2al}=\sqrt{2glsinθ}$,
则重力的瞬时功率为:$P=mgvsinθ=mgsinθ\sqrt{2glsinθ}$.
因为支持力的方向与速度方向垂直,则支持力做功的功率为零.
合力做功等于各力做功的代数和,则合力做功为:W=mgh=mglsinθ.
故答案为:mglsinθ,$mgsinθ\sqrt{\frac{glsinθ}{2}}$,$mgsinθ\sqrt{2glsinθ}$,0,mglsinθ
点评 本题考查了功率的基本运算,知道平均功率和瞬时功率的区别,掌握这两种功率的求法,难度不大.

练习册系列答案
相关题目
13.一物体在竖直弹簧的上方h米处下落,然后又被弹簧弹回,则物体动能最大时是( )
| A. | 物体刚接触弹簧时 | B. | 物体重力与弹力相等时 | ||
| C. | 物体将弹簧压缩至最短时 | D. | 弹簧等于原长时 |
8.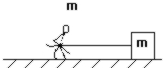 一只猴子用绳子拉着一块与其等质量的石块,在光滑水平面上运动(如图),开始时猴子和石块都静止,然后猴子以相对于绳子的速度u拉石块,则石块的速度为( )
一只猴子用绳子拉着一块与其等质量的石块,在光滑水平面上运动(如图),开始时猴子和石块都静止,然后猴子以相对于绳子的速度u拉石块,则石块的速度为( )
 一只猴子用绳子拉着一块与其等质量的石块,在光滑水平面上运动(如图),开始时猴子和石块都静止,然后猴子以相对于绳子的速度u拉石块,则石块的速度为( )
一只猴子用绳子拉着一块与其等质量的石块,在光滑水平面上运动(如图),开始时猴子和石块都静止,然后猴子以相对于绳子的速度u拉石块,则石块的速度为( )| A. | $\frac{u}{2}$ | B. | u | C. | $\frac{3}{2}u$ | D. | 2u |
9. 在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.在一段时间内,穿过螺线管的磁场的磁感应强度B(以向下为正)按如图乙所示的规律变化.则下列说法中正确的是( )
在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.在一段时间内,穿过螺线管的磁场的磁感应强度B(以向下为正)按如图乙所示的规律变化.则下列说法中正确的是( )
 在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.在一段时间内,穿过螺线管的磁场的磁感应强度B(以向下为正)按如图乙所示的规律变化.则下列说法中正确的是( )
在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2.螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.在一段时间内,穿过螺线管的磁场的磁感应强度B(以向下为正)按如图乙所示的规律变化.则下列说法中正确的是( )| A. | 螺线管中产生的感应电动势为1.2V | |
| B. | 闭合S,电路中的电流稳定后电容器上极板带正电 | |
| C. | S断开后,流经R2的电量为1.8×10-5C | |
| D. | 电路中的电流稳定后,电阻R1的电功率为5×10-2W |
6.一物体做匀变速直线运动,某时刻速度的大小为4m/s,1s后速度大小变为10m/s,在这1s内物体的以下说法错误的是( )
| A. | 平均速度的大小可能是7 m/s | B. | 位移的大小可能小于4 m | ||
| C. | 速度变化量大小可能小于4 m/s | D. | 加速度的大小可能小于10 m/s2 |
7. 如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
 如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )
如图是法拉第研制成的世界上第一台发电机模型的原理图.将铜盘放在磁场中,让磁感线垂直穿过铜盘,图中a、b导线与铜盘的中轴线处在同一平面内,转动铜盘,就可以使闭合电路获得电流.若图中铜盘半径为L,匀强磁场的磁感应强度为B,回路总电阻为R,从上往下看逆时针匀速转动铜盘的角速度为ω.则下列说法正确的是( )| A. | 本模型产生的感应电动势为BLω | |
| B. | 回路中电流方向不变,且从b导线流进灯泡,再从a流向旋转的铜盘 | |
| C. | 回路中有大小和方向作周期性变化的电流 | |
| D. | 若将匀强磁场改为仍然垂直穿过铜盘的正弦变化的磁场,不转动铜盘,灯泡中也会有电流流过 |

 如图所示,一个质子以初速度v0=5×106m/s射入一个由两块带电的平行金属板组成的区域.两板距离为20cm,金属板之间是匀强电场,电场强度为3×105V/m.质子质量为m=1.67×10-27kg,电荷量为q=1.60×10-19C.试求
如图所示,一个质子以初速度v0=5×106m/s射入一个由两块带电的平行金属板组成的区域.两板距离为20cm,金属板之间是匀强电场,电场强度为3×105V/m.质子质量为m=1.67×10-27kg,电荷量为q=1.60×10-19C.试求