题目内容
16. 质量为m的小球,用长为L的线悬挂在O点,在O点正下方处$\frac{L}{2}$有一光滑的钉子O′,把小球拉到与O′水平的位置A,摆线被钉子拦住,如图所示,将小球由静止释放,当摆球第一次通过最低点B时( )
质量为m的小球,用长为L的线悬挂在O点,在O点正下方处$\frac{L}{2}$有一光滑的钉子O′,把小球拉到与O′水平的位置A,摆线被钉子拦住,如图所示,将小球由静止释放,当摆球第一次通过最低点B时( )| A. | 小球速率突然变小 | B. | 小球的角速度突然变大 | ||
| C. | 小球的拉力突然变小 | D. | 小球的向心加速度突然变小 |
分析 由机械能守恒可知小球到达最低点的速度,小球离开钉子后仍做圆周运动,由向心力公式可得出绳子的拉力与小球转动半径的关系;由圆周运动的性质可知其线速度、角速度及向心加速度的大小关系.
解答 解:A、小球摆下后由机械能守恒$mgh=\frac{1}{2}m{v}^{2}$可知,因小球下降的高度相同,故小球到达最低点时的速度相同,故小球的线速度不变,故A错误;
B、小球通过最低点时,线速度不变,根据ω=$\frac{v}{r}$知,半径增大,则角速度减小,故B错误;
C、设钉子到球的距离为r,则$F-mg=m\frac{{v}^{2}}{r}$,故绳子的拉力$F=mg+m\frac{{v}^{2}}{r}$,因r增大,则绳子上的拉力变小,故C正确;
D、小球的向心加速度a=$\frac{{v}^{2}}{r}$,半径增大,故小球的向心加速度减小,故D正确;
故选:CD.
点评 本题中要注意细绳离开钉子后转动半径的变化,再由向心力公式分析绳子上的拉力变化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.关于向心加速度,下列说法正确的是( )
| A. | 它描述的是线速度方向变化的快慢 | |
| B. | 它描述的是线速度大小变化的快慢 | |
| C. | 在匀速圆周运动中,向心加速度的大小不变 | |
| D. | 在匀速圆周运动中,向心加速度的方向一直指向圆周运动的圆心 |
5.两个完全相同的电热器,分别通有如图A、B所示的交流电流,则它们的功率之比为( )


| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | 4:1 |
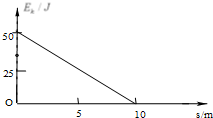 质量为2kg的物体以50J的初动能在粗糙的水平面上滑行,其动能变化与位移的关系如图所示,则物体在水平面上滑行的时间为$2\sqrt{2}$;若该物体以30J的初动能在同一粗糙的水平面上滑行时,其可滑行的最远距离为6m.
质量为2kg的物体以50J的初动能在粗糙的水平面上滑行,其动能变化与位移的关系如图所示,则物体在水平面上滑行的时间为$2\sqrt{2}$;若该物体以30J的初动能在同一粗糙的水平面上滑行时,其可滑行的最远距离为6m. 长为L的细绳,一端被固定于O点,另一端系住一个质量为m的小球,若让小球从图中的A点下摆至最低位置B点时,小球的重力所做的功是mgL(1-cosθ ).
长为L的细绳,一端被固定于O点,另一端系住一个质量为m的小球,若让小球从图中的A点下摆至最低位置B点时,小球的重力所做的功是mgL(1-cosθ ). 如图所示是自行车传动部分的结构示意图,牙盘A 通过链条和飞轮B相连,飞轮与后轮C同轴,已知牙盘A、飞轮B和后轮C的半径分别为20cm、10cm、30cm,则当人踩踏脚板使自行车以3m/s的速度在平直的水平路面上匀速前进时,求:
如图所示是自行车传动部分的结构示意图,牙盘A 通过链条和飞轮B相连,飞轮与后轮C同轴,已知牙盘A、飞轮B和后轮C的半径分别为20cm、10cm、30cm,则当人踩踏脚板使自行车以3m/s的速度在平直的水平路面上匀速前进时,求: 用三棱镜做测定玻璃折射率的实验,先在白纸上放好三棱镜,在棱镜的一侧插上两枚大头针P1和P2,然后在棱镜的另一侧观察,调整视线,使P2的像挡住P1的像,接着在眼睛所在的一侧插两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3和P1、P2的像.在纸上标出大头针位置的三棱镜如图所示:
用三棱镜做测定玻璃折射率的实验,先在白纸上放好三棱镜,在棱镜的一侧插上两枚大头针P1和P2,然后在棱镜的另一侧观察,调整视线,使P2的像挡住P1的像,接着在眼睛所在的一侧插两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3和P1、P2的像.在纸上标出大头针位置的三棱镜如图所示: