题目内容
1.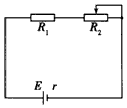 如图所示,已知电源的电动势E=5V,内阻r=2Ω,定值电阻R1=0.5Ω,滑动变阻器R2的最大阻值为10Ω.求:
如图所示,已知电源的电动势E=5V,内阻r=2Ω,定值电阻R1=0.5Ω,滑动变阻器R2的最大阻值为10Ω.求:(1)当滑动变阻器R2的阻值为多大时,电阻R1消耗的功率最大?
(2)当滑动变阻器R2的阻值为多大时,滑动变阻器消耗的功率最大?
(3)当滑动变阻器R2的阻值为多大时,电源的输出功率最大?最大功率为多少?
分析 (1)根据P=I2R,当电流最大时,定值电阻R1消耗的功率最大;
(2)对于电源,当外电路的电阻等于内电阻时电源的输出功率最大;将电阻R1与电源等效成等效电源考虑;
(3)当外电路的电阻等于内电阻时电源的输出功率最大,最大功率P=$\frac{{E}^{2}}{4r}$.
解答 解:(1)根据P=I2R,当电流最大时,电阻R1消耗的功率最大,故当滑动变阻器短路,即电阻值为零时,电阻R1消耗的功率最大;
(2)对于电源,当外电路的电阻等于内电阻时电源的输出功率最大;将电阻R1与电源等效成电源,故当滑动变阻器的阻值为2.5Ω时,滑动变阻器消耗的功率最大;
(3)当外电路的电阻等于内电阻时电源的输出功率最大,故当滑动变阻器的阻值为1.5Ω时,电源的输出功率最大;
最大功率为:Pm=$\frac{{E}^{2}}{4r}$=$\frac{{5}^{2}}{4×2}$=3.125W;
答:(1)当滑动变阻器的阻值为零时,电阻R1消耗的功率最大;
(2)当滑动变阻器的阻值为2.5Ω时,滑动变阻器消耗的功率最大;
(3)当滑动变阻器的阻值为1.5Ω时,电源的输出功率最大,最大功率为3.125W.
点评 本题采用结论法解题,关键记住“对于电源,当外电路的电阻等于内电阻时电源的输出功率最大”的结论应用,但要注意对于定值电阻的最大值要注意明确电流越大,功率越大.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
9.一同学要研究轻质弹簧的弹性势能与弹簧长度改变量的关系.实验装置如下图甲所示,在离地面高为h的光滑水平桌面上,沿着与桌子右边缘垂直的方向放置一轻质弹簧,其左端固定,右端与质量为m的小刚球接触.将小球向左压缩弹簧一段距离后由静止释放,使小球沿水平方向射出桌面,小球在空中飞行落到位于水平地面的记录纸上留下痕迹.重力加速度为g

(1)若测得某次压缩弹簧释放后小球落点P痕迹到O点的距离为s,则释放小球前弹簧的弹性势能表达式为$\frac{mg{s}^{2}}{4h}$;
(2)该同学改变弹簧的压缩量进行多次测量得到下表一组数据:
结合(1)问与表中数据,弹簧弹性势能与弹簧压缩量x之间的关系式应为$\frac{1{0}^{4}mg{x}^{2}}{h}$;
(3)完成实验后,该同学对上述装置进行了如图乙所示的改变:
(I)在木板表面先后钉上白纸和复写纸,并将木板竖直立于靠近桌子右边缘处,使小球向左压缩弹簧一段距离后由静止释放,撞到木板并在白纸上留下痕迹O;
(II)将木板向右平移适当的距离固定,再使小球向左压缩弹簧一段距离后由静止释放,撞到木板上得到痕迹P;
(III)用刻度尺测量纸上O点到P点的竖直距离为y.若已知木板与桌子右边缘的水平距离为L,则(II)步骤中弹簧的压缩量应该为$\frac{L}{200}$$\sqrt{\frac{h}{y}}$.

(1)若测得某次压缩弹簧释放后小球落点P痕迹到O点的距离为s,则释放小球前弹簧的弹性势能表达式为$\frac{mg{s}^{2}}{4h}$;
(2)该同学改变弹簧的压缩量进行多次测量得到下表一组数据:
| 弹簧压缩量x/cm | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
| 小球飞行水平距离s/×102cm | 2.01 | 3.00 | 4.01 | 4.98 | 6.01 | 6.99 |
(3)完成实验后,该同学对上述装置进行了如图乙所示的改变:
(I)在木板表面先后钉上白纸和复写纸,并将木板竖直立于靠近桌子右边缘处,使小球向左压缩弹簧一段距离后由静止释放,撞到木板并在白纸上留下痕迹O;
(II)将木板向右平移适当的距离固定,再使小球向左压缩弹簧一段距离后由静止释放,撞到木板上得到痕迹P;
(III)用刻度尺测量纸上O点到P点的竖直距离为y.若已知木板与桌子右边缘的水平距离为L,则(II)步骤中弹簧的压缩量应该为$\frac{L}{200}$$\sqrt{\frac{h}{y}}$.
16. 如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖直立在地面上的钢管往下滑,已知这名消防队员的质量为60kg,他从钢管顶端由静止开始先匀加速下滑后匀减速下滑,滑到地面时速度恰好为零.如果他加速时加速度大小是减速时的2倍,下滑的总时间为3s,g=10m/s2,那么该消防员( )
如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖直立在地面上的钢管往下滑,已知这名消防队员的质量为60kg,他从钢管顶端由静止开始先匀加速下滑后匀减速下滑,滑到地面时速度恰好为零.如果他加速时加速度大小是减速时的2倍,下滑的总时间为3s,g=10m/s2,那么该消防员( )
 如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖直立在地面上的钢管往下滑,已知这名消防队员的质量为60kg,他从钢管顶端由静止开始先匀加速下滑后匀减速下滑,滑到地面时速度恰好为零.如果他加速时加速度大小是减速时的2倍,下滑的总时间为3s,g=10m/s2,那么该消防员( )
如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖直立在地面上的钢管往下滑,已知这名消防队员的质量为60kg,他从钢管顶端由静止开始先匀加速下滑后匀减速下滑,滑到地面时速度恰好为零.如果他加速时加速度大小是减速时的2倍,下滑的总时间为3s,g=10m/s2,那么该消防员( )| A. | 下滑过程中的最大速度为4m/s | |
| B. | 加速与减速过程中所受摩擦力大小之比为1:7 | |
| C. | 加速与减速过程的时间之比为1:4 | |
| D. | 加速与减速过程的位移大小之比为1:4 |
6. 如图所示的是表演“水流星”节目的示意图,拴杯子的绳子长为l,绳子能够承受的最大拉力是杯子和杯内水重力的8 倍,要使绳子不断,节目获得成功,则杯子通过最高点时速度的最小值和通过最低点时速度的最大值分别为( )
如图所示的是表演“水流星”节目的示意图,拴杯子的绳子长为l,绳子能够承受的最大拉力是杯子和杯内水重力的8 倍,要使绳子不断,节目获得成功,则杯子通过最高点时速度的最小值和通过最低点时速度的最大值分别为( )
 如图所示的是表演“水流星”节目的示意图,拴杯子的绳子长为l,绳子能够承受的最大拉力是杯子和杯内水重力的8 倍,要使绳子不断,节目获得成功,则杯子通过最高点时速度的最小值和通过最低点时速度的最大值分别为( )
如图所示的是表演“水流星”节目的示意图,拴杯子的绳子长为l,绳子能够承受的最大拉力是杯子和杯内水重力的8 倍,要使绳子不断,节目获得成功,则杯子通过最高点时速度的最小值和通过最低点时速度的最大值分别为( )| A. | $\sqrt{gl}$$\sqrt{7gl}$ | B. | $\sqrt{7gl}$$\sqrt{gl}$ | C. | 0 $\sqrt{gl}$ | D. | 0 $\sqrt{7gl}$ |
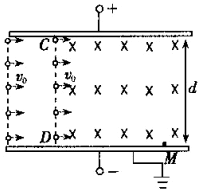 空气中的颗粒物对人体健康有重要影响.有人利用除尘器对空气除尘,除尘器主要由过滤器、离子发生器(使颗粒物带电)、集尘器组成.如图所示为集尘器的截面 图,间距为d的上、下两板与直流电源相连,CD为匀强磁场的左边界,磁场的方向垂直纸面向里.质量均为m、带相等电荷量分布均匀的颗粒物,以水平速度v0进入集尘器,调节电源电压至U,颗粒物在电场区域恰能沿水平向右做匀速直线运动,再进入电场、磁场共存区域后颗粒物偏转碰到下板后其电量消失,同时被收集,设重力加速度为g,不计颗粒物之间的相互作用.
空气中的颗粒物对人体健康有重要影响.有人利用除尘器对空气除尘,除尘器主要由过滤器、离子发生器(使颗粒物带电)、集尘器组成.如图所示为集尘器的截面 图,间距为d的上、下两板与直流电源相连,CD为匀强磁场的左边界,磁场的方向垂直纸面向里.质量均为m、带相等电荷量分布均匀的颗粒物,以水平速度v0进入集尘器,调节电源电压至U,颗粒物在电场区域恰能沿水平向右做匀速直线运动,再进入电场、磁场共存区域后颗粒物偏转碰到下板后其电量消失,同时被收集,设重力加速度为g,不计颗粒物之间的相互作用. 如图甲所示,光滑的水平地面上放有一质量为M、长为L=4.0m的木板.从t=0时刻开始,质量为m=1.0kg的物块以初速度v0=6m/s从左侧滑上木板,同时在木板上施以水平向右的恒力F=7.0N.已知开始运动后第1s内两物体的图线如图乙所示,物块可视为质点.g=10m/s2.求:
如图甲所示,光滑的水平地面上放有一质量为M、长为L=4.0m的木板.从t=0时刻开始,质量为m=1.0kg的物块以初速度v0=6m/s从左侧滑上木板,同时在木板上施以水平向右的恒力F=7.0N.已知开始运动后第1s内两物体的图线如图乙所示,物块可视为质点.g=10m/s2.求: 以某一初速度水平抛出一物体,若以抛出点为坐标原点O,初速度方向为x轴的正方向,物体所受重力方向为y轴的正方向,建立如图所示坐标系.它的运动轨迹满足方程y=0.05x2,经过一段时间物体的速度大小变为初速度的$\sqrt{2}$倍,不计空气阻力,取g=10m/s2,求:
以某一初速度水平抛出一物体,若以抛出点为坐标原点O,初速度方向为x轴的正方向,物体所受重力方向为y轴的正方向,建立如图所示坐标系.它的运动轨迹满足方程y=0.05x2,经过一段时间物体的速度大小变为初速度的$\sqrt{2}$倍,不计空气阻力,取g=10m/s2,求: 汽车由静止开始在平直的公路上行驶,0~50s内汽车的加速度随时间变化的图线如图所示.求:
汽车由静止开始在平直的公路上行驶,0~50s内汽车的加速度随时间变化的图线如图所示.求: