题目内容
19. 如图所示,在0≤x≤b、0≤y≤a的长方形区域中有一磁感应强度大小为B的匀强磁场,磁场的方向垂直于xOy平面向外.O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xOy平面内的第一象限内(包括ox、oy轴).若粒子在磁场中做圆周运动的周期为T,最先从磁场上边界飞出的粒子经历的时间为$\frac{T}{12}$,最后从磁场中飞出的粒子经历的时间为$\frac{T}{4}$.不计粒子的重力及粒子间的相互作用,则
如图所示,在0≤x≤b、0≤y≤a的长方形区域中有一磁感应强度大小为B的匀强磁场,磁场的方向垂直于xOy平面向外.O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xOy平面内的第一象限内(包括ox、oy轴).若粒子在磁场中做圆周运动的周期为T,最先从磁场上边界飞出的粒子经历的时间为$\frac{T}{12}$,最后从磁场中飞出的粒子经历的时间为$\frac{T}{4}$.不计粒子的重力及粒子间的相互作用,则(1)粒子的入磁场的速度大小为多少?
(2)求长方形区域的边长满足关系.
分析 (1)根据题意,粒子运动时间最短时,其回旋的角度最小,画出运动轨迹,根据几何关系列出方程求解出轨道半径,再根据洛伦兹力提供向心力得出速度大小;
(2)最后离开磁场的粒子,其运动时间最长,由题意画出运动的轨迹,故可以根据几何关系列出方程求变长之间的关系.
解答 解(1)最先从磁场上边界中飞出的带电粒子的运动轨迹可如图表示:
可知此时粒子在磁场中偏转的圆心角为30°,根据几何关系得粒子运动的半径r=2a,
根据牛顿第二定律有:qvB=m$\frac{{v}^{2}}{r}$,
粒子的射入磁场的速度大小:v=$\frac{2qBa}{m}$;
(2)最后从磁场中飞出的带电粒子在磁场中的运动轨迹可如图表示:
设发射方向与y轴正方向的夹角为α,根据几何关系有:
rsinα=r-a,rsinα=b-rcosα,解得:α=30°,b=(1+$\sqrt{3}$)a;
答:(1)粒子的入磁场的速度大小为$\frac{2qBa}{m}$.
(2)长方形区域的边长满足关系为:b=(1+$\sqrt{3}$)a.
点评 本题关键是画出运动时间最短的粒子的运动轨迹,然后根据几何关系得到轨道半径,再根据洛仑兹力提供向心力得到速度大小.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
6.如图是电阻R的I-U图线,图中α=45°,由此得出( )


| A. | 通过电阻的电流大,电阻就小 | |
| B. | 加在电阻两端的电压大,电阻就大 | |
| C. | 因I-U图线的斜率表示电阻的倒数,故R=cot α=1.0Ω | |
| D. | 在R两端加6V电压时,每秒通过电阻横截面的电荷量是3 C |
11. 一列简谐横波在t=0时刻的波形如图中的实线所示,t=0.02s时刻的波形如图中虚线所示,则下列说法正确的是 ( )
一列简谐横波在t=0时刻的波形如图中的实线所示,t=0.02s时刻的波形如图中虚线所示,则下列说法正确的是 ( )
 一列简谐横波在t=0时刻的波形如图中的实线所示,t=0.02s时刻的波形如图中虚线所示,则下列说法正确的是 ( )
一列简谐横波在t=0时刻的波形如图中的实线所示,t=0.02s时刻的波形如图中虚线所示,则下列说法正确的是 ( )| A. | 如果波向右传播,波速一定为1m/s | |
| B. | 如果波向右传播,波速可能为5m/s | |
| C. | 如果波向左传播,最小波速为3m/s | |
| D. | 如果波向左传播,波速一定是3m/s的整数倍 |
9.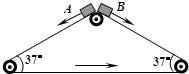 如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m,且与水平方向的夹角均为37°.现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,两物块与传送带的动摩擦因数都是0.5,g=10m/s2,sin37°=0.6,cos37°=0.8.下列判断不正确的是( )
如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m,且与水平方向的夹角均为37°.现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,两物块与传送带的动摩擦因数都是0.5,g=10m/s2,sin37°=0.6,cos37°=0.8.下列判断不正确的是( )
 如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m,且与水平方向的夹角均为37°.现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,两物块与传送带的动摩擦因数都是0.5,g=10m/s2,sin37°=0.6,cos37°=0.8.下列判断不正确的是( )
如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m,且与水平方向的夹角均为37°.现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,两物块与传送带的动摩擦因数都是0.5,g=10m/s2,sin37°=0.6,cos37°=0.8.下列判断不正确的是( )| A. | 物块A先到达传送带底端 | |
| B. | 物块AB同时到达传送带底端 | |
| C. | 传送带对物块AB的摩擦力都沿传送带向上 | |
| D. | 物块A下滑过程中相对传送带的位移小于物块B下滑过程中相对传送带的位移 |
 在一次测定玻璃的折射率的实验中,采用了如下方法:
在一次测定玻璃的折射率的实验中,采用了如下方法: 在现代科学实验室中,经常用磁场来控制带电粒子的运动.某仪器的内部结构简化如图:宽度为L的Ⅰ、Ⅱ两处的条形匀强磁场区边界竖直,相距也为L,磁场方向相反且垂直于纸面.一质量为m、电量为-q(重力不计)的粒子以速度v平行于纸面射入Ⅰ区,射入时速度与水平方向夹角θ=30°.
在现代科学实验室中,经常用磁场来控制带电粒子的运动.某仪器的内部结构简化如图:宽度为L的Ⅰ、Ⅱ两处的条形匀强磁场区边界竖直,相距也为L,磁场方向相反且垂直于纸面.一质量为m、电量为-q(重力不计)的粒子以速度v平行于纸面射入Ⅰ区,射入时速度与水平方向夹角θ=30°.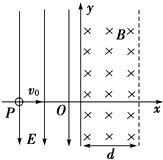 如图所示的空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种分界线,图中虚线为磁场区的右边界,现有一质量为m、带电量为-q的带电粒子(不计重力),从电场中P点以初速度v0沿x轴正方向运动.已知P点的坐标为(-L,0),且L=$\frac{mvθ}{Eq}$.试求:
如图所示的空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,y轴为两种分界线,图中虚线为磁场区的右边界,现有一质量为m、带电量为-q的带电粒子(不计重力),从电场中P点以初速度v0沿x轴正方向运动.已知P点的坐标为(-L,0),且L=$\frac{mvθ}{Eq}$.试求: