题目内容
11.用m表示地球同步通信卫星的质量、h表示卫星离地面的高度、M表示地球的质量、R0表示地球的半径、g0表示地球表面处的重力加速度、T0表示地球自转的周期、ω0表示地球自转的角速度,则地球同步通信卫星的环绕速度v为( )| A. | ω0(R0+h) | B. | $\sqrt{\frac{GM}{{R}_{0}+h}}$ | C. | $\root{3}{Gm{ω}_{0}}$ | D. | $\root{3}{{\frac{2πGM}{T_0}}}$ |
分析 由题地球的同步卫星的轨道半径为R=R0+h,根据万有引力等于向心力,由向心力公式求解线速度,也可以根据v=ωr求解.
解答 解:A、根据v=ωr得:线速度v=ω0(R0+h),故A正确;
B、根据万有引力提供向心力:$G\frac{Mm}{({R}_{0}+h)}=m\frac{{v}^{2}}{({R}_{0}+h)}$得:v=$\sqrt{\frac{GM}{{R}_{0}+h}}$,故B正确.
D、v=$\sqrt{\frac{GM}{{R}_{0}+h}}$=ω0(R0+h),
解得:
v=$\sqrt{\frac{GM}{\frac{v}{{ω}_{0}}}}$而${ω}_{0}=\frac{2π}{{T}_{0}}$
解得:v=$\root{3}{GM{ω}_{0}}$=$\root{3}{\frac{2πGM}{{T}_{0}}}$,故C错误,D正确;
故选:ABD
点评 本题为天体运动的典型题型,由万有引力提供向心力,再根据向心力的基本公式求解,难度不大,属于基础题.

练习册系列答案
相关题目
2.已知地球半径为R,质量为M,地面附近的重力加速度为g,万有引力恒量为G.那么第一宇宙速度的表达式及大小为( )
| A. | $\sqrt{\frac{R}{g}}$ | B. | $\sqrt{\frac{GM}{R}}$ | C. | 7.9km/s | D. | 11.2km/s |
6.洗衣机的甩干筒在旋转时有衣服附在筒壁上,则此时( )


| A. | 衣服受重力,筒壁的弹力和摩擦力,及离心力作用 | |
| B. | 衣服随筒壁做圆周运动的向心力由筒壁的弹力提供 | |
| C. | 筒壁对衣服的摩擦力随转速的增大而增大 | |
| D. | 筒壁对衣服的弹力随着衣服含水量的减少而减少 |
16. 如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体( )
如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体( )
 如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体( )
如图所示,质量相同的两个小物体A、B处于同一高度.现使A沿固定的光滑斜面无初速地自由下滑,而使B无初速地自由下落,最后A、B都运动到同一水平地面上.不计空气阻力.则在上述过程中,A、B两物体( )| A. | 所受重力冲量的大小相同 | B. | 所受合力冲量的大小相同 | ||
| C. | 所受重力做的功相同 | D. | 所受合力做的功相同 |
20. 如图所示,在质量为10kg的电动机上装有质量为1kg的偏心轮,偏心轮的重心离转轴的距离为0.5m,g取10m/s2.当偏心轮以4rad/s的角速度匀速转动时,有( )
如图所示,在质量为10kg的电动机上装有质量为1kg的偏心轮,偏心轮的重心离转轴的距离为0.5m,g取10m/s2.当偏心轮以4rad/s的角速度匀速转动时,有( )
 如图所示,在质量为10kg的电动机上装有质量为1kg的偏心轮,偏心轮的重心离转轴的距离为0.5m,g取10m/s2.当偏心轮以4rad/s的角速度匀速转动时,有( )
如图所示,在质量为10kg的电动机上装有质量为1kg的偏心轮,偏心轮的重心离转轴的距离为0.5m,g取10m/s2.当偏心轮以4rad/s的角速度匀速转动时,有( )| A. | 当偏心轮的重心转至转轴正下方时,转轴给偏心轮的作用力大小为18N,方向竖直向上 | |
| B. | 当偏心轮的重心转至转轴正上方时,转轴给偏心轮的作用力大小为2N,方向竖直向下 | |
| C. | 当偏心轮的重心转至转轴正下方时,电动机对地面的压力最大 | |
| D. | 无论偏心轮转动的角速度多大,电动机都不会离开地面 |
1. 如图所示为一皮带传动装置,右轮的半径为r,A是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,B点在小轮上,到小轮中心的距离为r,C点和D点分别位于小轮和大轮的边缘上.若在转动过程中,皮带不打滑,则( )
如图所示为一皮带传动装置,右轮的半径为r,A是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,B点在小轮上,到小轮中心的距离为r,C点和D点分别位于小轮和大轮的边缘上.若在转动过程中,皮带不打滑,则( )
 如图所示为一皮带传动装置,右轮的半径为r,A是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,B点在小轮上,到小轮中心的距离为r,C点和D点分别位于小轮和大轮的边缘上.若在转动过程中,皮带不打滑,则( )
如图所示为一皮带传动装置,右轮的半径为r,A是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,B点在小轮上,到小轮中心的距离为r,C点和D点分别位于小轮和大轮的边缘上.若在转动过程中,皮带不打滑,则( )| A. | A点与B点的线速度大小相等 | B. | C、D两点与B点的角速度大小相等 | ||
| C. | A点与C点的线速度大小相等 | D. | A点与D点的向心加速度大小相等 |
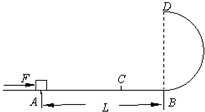 如图所示,固定在竖直面内的光滑半圆形轨道与粗糙水平轨道在B点平滑连接.轨道半径R=0.5m,一质量m=0.2kg的小物块(可视为质点)放在水平轨道上的A点,A与B相距L=10m,物块与水平轨道间的动摩擦因数μ=0.1.现用一水平恒力F向右推物块.已知F=3N,当物块运动到C点时撤去该力,设C点到A点的距离为x.在圆轨道的最高点D处安装一压力传感器,当物块运动到D点时传感器就会显示相应的读数FN,压力传感器所能承受的最大压力为90N,g取10m/s2.求:要使物块能够通过圆轨道的最高点D,求x的范围.
如图所示,固定在竖直面内的光滑半圆形轨道与粗糙水平轨道在B点平滑连接.轨道半径R=0.5m,一质量m=0.2kg的小物块(可视为质点)放在水平轨道上的A点,A与B相距L=10m,物块与水平轨道间的动摩擦因数μ=0.1.现用一水平恒力F向右推物块.已知F=3N,当物块运动到C点时撤去该力,设C点到A点的距离为x.在圆轨道的最高点D处安装一压力传感器,当物块运动到D点时传感器就会显示相应的读数FN,压力传感器所能承受的最大压力为90N,g取10m/s2.求:要使物块能够通过圆轨道的最高点D,求x的范围. 某正弦交流电电流随时间变化的图象如图所示,该交流电的频率为50Hz,周期T=0.02s.t=3ms时线圈平面和磁感线平行.(填平行或垂直)
某正弦交流电电流随时间变化的图象如图所示,该交流电的频率为50Hz,周期T=0.02s.t=3ms时线圈平面和磁感线平行.(填平行或垂直)