题目内容
15. 无限长光滑平行导轨MN、PQ水平放置,匀强垂直纸面向里,直金属棒a、b的长度、质量、电阻的关系为La=2Lb,ma=2mb,R=2Rb,开始时两棒的距离比较远,使两棒同时获得向右va=v0和向左vb=2v0的相向速度,且两棒在运动过程中始终平行并与导轨垂直.求在以后的运动过程中,金属棒b的最小速度.
无限长光滑平行导轨MN、PQ水平放置,匀强垂直纸面向里,直金属棒a、b的长度、质量、电阻的关系为La=2Lb,ma=2mb,R=2Rb,开始时两棒的距离比较远,使两棒同时获得向右va=v0和向左vb=2v0的相向速度,且两棒在运动过程中始终平行并与导轨垂直.求在以后的运动过程中,金属棒b的最小速度.
分析 a、b两棒最终做匀速直线运动,b棒匀速运动时的速度最小,根据导体切割磁感应线产生的感应电动势计算公式得出最终的速度关系,再根据动量定理列方程求解.
解答 解:设a最终的速度为v1、b最终的速度为v2,最后a、b均匀速运动,回路中的感应电流为零;
根据导体切割磁感应线产生的感应电动势计算公式可得:B•2lv1=Blv2,
设b的质量为m,则a的质量为2m,设从开始运动到达到稳定状态,回路中的平均感应电流为I,规定向左为正方向,根据动量定理可得:
对a棒:BI•2lt=2mv1-2m(-v0),
对b棒:-BIlt=mv2-m•2v0,
联立解得:v2=$\frac{2}{3}{v}_{0}$.
答:金属棒b的最小速度为$\frac{2}{3}{v}_{0}$.
点评 解决本题的关键知道最终金属棒做匀速运动,回路中感应电流为零,得出两者的速度关系是关键,运用动量定理进行求解,有一定的难度.

练习册系列答案
相关题目
1.3kg物体,从高45m处自由落下(g取10m/s2)在下落的过程中( )
| A. | 前2 s内重力做功的功率为300 W | B. | 前2 s内重力做功的功率为675 W | ||
| C. | 第2 s末重力做功的功率为600 W | D. | 第2 s末重力做功的功率为900 W |
7.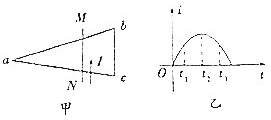 等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )
等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )
 等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )
等腰三角形线框abc与长直导线MN绝缘,且线框被导线分成面积相等的两部分,如图甲所示,MN中通有由N流向M的电流,电流强度随时间的变化如图乙所示,则关于线框中感应电流的判断正确的是( )| A. | 在任何时刻线框中都无感应电流 | |
| B. | 在t1时刻线框中有沿acba方向的感应电流 | |
| C. | 在t2时刻线框中有沿acba方向的感应电流 | |
| D. | 在t3时刻线框中有沿abca方向的感应电流 |
4.质量是15kg的小汽车在水平路面上滑行18m后速度从10m/s减小到8m/s,则小车所受的阻力为( )
| A. | 10N | B. | 15N | C. | 20N | D. | 25N |
5. 如图甲所示,倾角θ=30°的光滑斜面固定在水平面上,自然伸长的轻质弹簧一端固定在斜面底端的挡板上,一质量为m的小球,从离弹簧上端一定距离的位置静止释放,接触弹簧后继续向下运动,小球运动的v-t图象如图乙所示,其中OA段为直线,ABC段是与OA相切于A点的平滑曲线,不考虑空气阻力,重力加速度为g,关于小球的运动过程,下列说法正确的是( )
如图甲所示,倾角θ=30°的光滑斜面固定在水平面上,自然伸长的轻质弹簧一端固定在斜面底端的挡板上,一质量为m的小球,从离弹簧上端一定距离的位置静止释放,接触弹簧后继续向下运动,小球运动的v-t图象如图乙所示,其中OA段为直线,ABC段是与OA相切于A点的平滑曲线,不考虑空气阻力,重力加速度为g,关于小球的运动过程,下列说法正确的是( )
 如图甲所示,倾角θ=30°的光滑斜面固定在水平面上,自然伸长的轻质弹簧一端固定在斜面底端的挡板上,一质量为m的小球,从离弹簧上端一定距离的位置静止释放,接触弹簧后继续向下运动,小球运动的v-t图象如图乙所示,其中OA段为直线,ABC段是与OA相切于A点的平滑曲线,不考虑空气阻力,重力加速度为g,关于小球的运动过程,下列说法正确的是( )
如图甲所示,倾角θ=30°的光滑斜面固定在水平面上,自然伸长的轻质弹簧一端固定在斜面底端的挡板上,一质量为m的小球,从离弹簧上端一定距离的位置静止释放,接触弹簧后继续向下运动,小球运动的v-t图象如图乙所示,其中OA段为直线,ABC段是与OA相切于A点的平滑曲线,不考虑空气阻力,重力加速度为g,关于小球的运动过程,下列说法正确的是( )| A. | 小球在tB时刻所受弹簧弹力等于0.5mg | |
| B. | 整个过程小球的机械能守恒 | |
| C. | 小球从tC时刻所在的位置由静止释放后,不能回到出发点 | |
| D. | 小球从tA时刻到tC时刻的过程中重力势能的减少量小于弹簧弹性势能的增加量 |
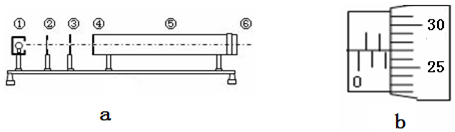
 如图所示,a、b、c、d分别是四根半径都为R、表面光滑的圆柱体的横截面,彼此靠得很近,形成四个宽度极窄的狭缝1、2、3、4;在这些狭缝和四个圆柱所包围的空间内存在匀强磁场,磁场方向垂直于纸面指向纸里,整个空间为真空.质量为m、电荷量为q的带正电的粒子,从A点由静止经电压为U的电场加速后,沿与a、b都相切的方向由缝1射入磁场,恰好能从缝2沿与b、c都相切的方向射出.设粒子与圆柱表面只发生一次碰撞,碰撞后粒子的速度大小不变,方向相反,碰撞时间极短,且碰撞不改变粒子的电荷量,不计粒子的重力.求:
如图所示,a、b、c、d分别是四根半径都为R、表面光滑的圆柱体的横截面,彼此靠得很近,形成四个宽度极窄的狭缝1、2、3、4;在这些狭缝和四个圆柱所包围的空间内存在匀强磁场,磁场方向垂直于纸面指向纸里,整个空间为真空.质量为m、电荷量为q的带正电的粒子,从A点由静止经电压为U的电场加速后,沿与a、b都相切的方向由缝1射入磁场,恰好能从缝2沿与b、c都相切的方向射出.设粒子与圆柱表面只发生一次碰撞,碰撞后粒子的速度大小不变,方向相反,碰撞时间极短,且碰撞不改变粒子的电荷量,不计粒子的重力.求: 如图所示,仅在矩形金属线框内有垂直于线框平面的匀强磁场,线框的长边与短边长度之比为4:1.现用两种方法将线框从磁场中拉出一种方法是以速度v1沿短边方向匀速拉出,在拉出过程中感应电流做功为W1,通过导线横截面的电量为q1,另一种方法是以速度v2沿长边方向匀速拉出,拉出过程中感应电流做功为W2,通过导线横截面的电量为q2,若v1=2v2,则W1:W2=8:1,q1:q2=1:1.
如图所示,仅在矩形金属线框内有垂直于线框平面的匀强磁场,线框的长边与短边长度之比为4:1.现用两种方法将线框从磁场中拉出一种方法是以速度v1沿短边方向匀速拉出,在拉出过程中感应电流做功为W1,通过导线横截面的电量为q1,另一种方法是以速度v2沿长边方向匀速拉出,拉出过程中感应电流做功为W2,通过导线横截面的电量为q2,若v1=2v2,则W1:W2=8:1,q1:q2=1:1. 如图,光滑的竖直导轨放置于匀强磁场B中,宽为L,放有一根导体棒ab,其接入导轨电阻为r,由静止开始运动,外电阻为R,分析ab的受力情况和运动情况,并求出ab的最大速度.
如图,光滑的竖直导轨放置于匀强磁场B中,宽为L,放有一根导体棒ab,其接入导轨电阻为r,由静止开始运动,外电阻为R,分析ab的受力情况和运动情况,并求出ab的最大速度.