题目内容
12. 如图所示,一固定竖直轨道由半径为R的四分之一圆弧AB、长度为L的水平直轨BC和半径为r的四分之一圆弧CD构成,BC与两网弧分别相切于B点和C点.质量为Ⅲ的质点物块从A点由静止释放,恰好能到达D点,已知物块在圆弧AB上克服摩擦力做的功为Wl,在圆弧CD上克服摩擦力做的功为W2,重力加速度大小为g,则( )
如图所示,一固定竖直轨道由半径为R的四分之一圆弧AB、长度为L的水平直轨BC和半径为r的四分之一圆弧CD构成,BC与两网弧分别相切于B点和C点.质量为Ⅲ的质点物块从A点由静止释放,恰好能到达D点,已知物块在圆弧AB上克服摩擦力做的功为Wl,在圆弧CD上克服摩擦力做的功为W2,重力加速度大小为g,则( )| A. | 物块在水平直轨上的动摩擦因数为$\frac{R+r}{L}$-$\frac{{W}_{1}+{W}_{2}}{mgL}$ | |
| B. | 物块在水平直轨上的动摩擦因数为$\frac{R-r}{L}$-$\frac{{W}_{1}+{W}_{2}}{mgL}$ | |
| C. | 物块在C点的向心加速度的大小为2g+$\frac{{2W}_{2}}{mr}$ | |
| D. | 物块在C点的向心加速度的大小为2g+$\frac{2({W}_{1}+{W}_{2})}{mr}$ |
分析 (1)对于ABCD整个过程,根据动能定理求出物块在水平直轨上的动摩擦因数;
(2)对于ABC过程利用动能定理并结合向心力公式列式,可求出物块在C点的向心加速度的大小.
解答 解:AB、设物块在水平直轨上克服摩擦力做的功为W3,对于ABCD整个过程,由动能定理得:mg(R-r)-(W1+W2+W3)=0…①
又因为W3=μmgL…②
联立①②式可得:μ=$\frac{R-r}{L}$-$\frac{{W}_{1}+{W}_{2}}{mgL}$,故A错误,B正确;
CD、对于ABC过程有:mgR-(W1+W3)=$\frac{1}{2}m{v}_{C}^{2}$-0…③
由向心加速度公式得:a=$\frac{{v}_{C}^{2}}{r}$…④
练力量①③④式可得:a=2g+$\frac{2{W}_{2}}{mr}$,故C正确,D错误.
故选:BC.
点评 本题考查动能定理和向心力公式的综合应用,关键要弄清物块在不同阶段满足的规律,灵活选择相关公式即可正确解题,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.一物块从某一高度水平抛出,落地时的速度方向与水平方向的夹角为$\frac{π}{4}$,取水平地面为重力势能零点,不计空气阻力,下列叙述中正确的是( )
| A. | 物块水平抛出时的动能与重力势能相等 | |
| B. | 落地时的重力功率是水平抛出时重力功率的两倍 | |
| C. | 落地时的速度大小为水平初速度大小的两倍 | |
| D. | 重力做功的大小是水平抛出时物块动能的两倍. |
3. 洛伦兹力的方向可用左手定则判断.一正电荷垂直于如图所示的匀强磁场运动时,所受的洛伦兹力向上.则此时它的运动方向是( )
洛伦兹力的方向可用左手定则判断.一正电荷垂直于如图所示的匀强磁场运动时,所受的洛伦兹力向上.则此时它的运动方向是( )
 洛伦兹力的方向可用左手定则判断.一正电荷垂直于如图所示的匀强磁场运动时,所受的洛伦兹力向上.则此时它的运动方向是( )
洛伦兹力的方向可用左手定则判断.一正电荷垂直于如图所示的匀强磁场运动时,所受的洛伦兹力向上.则此时它的运动方向是( )| A. | 向上 | B. | 向下 | C. | 向左 | D. | 向右 |
2. 有三颗卫星运动于如图所示的三个轨道,其中轨道1和轨道3是以地球为圆心的圆,轨道2 是椭圆轨道,且地球在其中的一个焦点上,轨道2分别与轨道1和轨道3相切于Q和P点,卫星在运动过程中不会相撞,则下列分析正确的是( )
有三颗卫星运动于如图所示的三个轨道,其中轨道1和轨道3是以地球为圆心的圆,轨道2 是椭圆轨道,且地球在其中的一个焦点上,轨道2分别与轨道1和轨道3相切于Q和P点,卫星在运动过程中不会相撞,则下列分析正确的是( )
 有三颗卫星运动于如图所示的三个轨道,其中轨道1和轨道3是以地球为圆心的圆,轨道2 是椭圆轨道,且地球在其中的一个焦点上,轨道2分别与轨道1和轨道3相切于Q和P点,卫星在运动过程中不会相撞,则下列分析正确的是( )
有三颗卫星运动于如图所示的三个轨道,其中轨道1和轨道3是以地球为圆心的圆,轨道2 是椭圆轨道,且地球在其中的一个焦点上,轨道2分别与轨道1和轨道3相切于Q和P点,卫星在运动过程中不会相撞,则下列分析正确的是( )| A. | 在Q点时,卫星1和卫星2受到的地球引力一定相同 | |
| B. | 在P点时,卫星2和卫星3具有相同的加速度 | |
| C. | 卫星2在P、Q两点的线速度大小相同 | |
| D. | 卫星1在Q的线速度大于卫星2在Q点的线速度 |
 如图为某质点做直线运动的v-t图象,0~5s内质点做匀加速(填“匀速”或“匀加速”)直线运动;0~5s内质点的平均速度大小为5m/s;8s末质点的瞬时速度大小为10m/s.
如图为某质点做直线运动的v-t图象,0~5s内质点做匀加速(填“匀速”或“匀加速”)直线运动;0~5s内质点的平均速度大小为5m/s;8s末质点的瞬时速度大小为10m/s.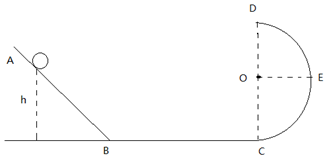
 如图为某古法榨油装置,轻杆O1A可绕O1轴转动,A端重物质量为10kg,下拉A可通过滑轮O2将重物P提起,释放A,P下落至平台Q,对固定的平台上的油饼进行捶压,已知P的质量为30kg,O1O2=3m,O1A=5m.将重物A拉到O1A杆水平时释放,当杆转到A与O2等高时,若系统减小的重力势能有240J转化为动能,则重物P此时的速度最接近2.9m/s.
如图为某古法榨油装置,轻杆O1A可绕O1轴转动,A端重物质量为10kg,下拉A可通过滑轮O2将重物P提起,释放A,P下落至平台Q,对固定的平台上的油饼进行捶压,已知P的质量为30kg,O1O2=3m,O1A=5m.将重物A拉到O1A杆水平时释放,当杆转到A与O2等高时,若系统减小的重力势能有240J转化为动能,则重物P此时的速度最接近2.9m/s.