题目内容
2.一物块从某一高度水平抛出,落地时的速度方向与水平方向的夹角为$\frac{π}{4}$,取水平地面为重力势能零点,不计空气阻力,下列叙述中正确的是( )| A. | 物块水平抛出时的动能与重力势能相等 | |
| B. | 落地时的重力功率是水平抛出时重力功率的两倍 | |
| C. | 落地时的速度大小为水平初速度大小的两倍 | |
| D. | 重力做功的大小是水平抛出时物块动能的两倍. |
分析 根据落地时的速度方向与水平方向的夹角为$\frac{π}{4}$,得到落地时水平分速度与竖直分速度的关系,由运动学公式得到下落的高度与水平速度的关系,从而求得物块水平抛出时的动能与重力势能关系.根据功率公式P=Fvcosα分析落地时的重力功率与水平抛出时重力功率关系.根据动能定理研究重力做功与水平抛出时物块动能关系.
解答 解:A、设物块落地时速度大小为v,竖直分速度大小为vy,初速度为v0.据题有 vy=v0.
物体下落的高度为 h=$\frac{{v}_{y}^{2}}{2g}$=$\frac{{v}_{0}^{2}}{2g}$
所以物块水平抛出时的重力势能为 Ep=mgh=$\frac{1}{2}m{v}_{0}^{2}$,即物块水平抛出时的动能与重力势能相等,故A正确.
B、落地时的重力功率是 P=mgvy=mgv0,水平抛出时重力与速度垂直,重力功率为零,故B错误.
C、落地时的速度大小 v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{2}{v}_{0}$,故C错误.
D、重力做功的大小为 W=mgh=$\frac{1}{2}m{v}_{0}^{2}$,即重力做功的大小与水平抛出时物块动能相等,故D错误.
故选:A
点评 解决本题的关键是掌握平抛运动的研究方法:运动的分解,要注意重力做功的功率与竖直分速度有关.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
13. 如图所示,重球系于细绳DC下端,重球下再系一根同样的细绳BA,在细绳的A端缓慢增加拉力,下列说法正确的是( )
如图所示,重球系于细绳DC下端,重球下再系一根同样的细绳BA,在细绳的A端缓慢增加拉力,下列说法正确的是( )
 如图所示,重球系于细绳DC下端,重球下再系一根同样的细绳BA,在细绳的A端缓慢增加拉力,下列说法正确的是( )
如图所示,重球系于细绳DC下端,重球下再系一根同样的细绳BA,在细绳的A端缓慢增加拉力,下列说法正确的是( )| A. | 细绳DC先断 | |
| B. | 细绳BA先断 | |
| C. | 细绳断开前,细绳DC的拉力总大于细绳BA的拉力 | |
| D. | 细绳断开前,细绳DC的拉力总小于细绳BA的拉力 |
12. 如图所示,一固定竖直轨道由半径为R的四分之一圆弧AB、长度为L的水平直轨BC和半径为r的四分之一圆弧CD构成,BC与两网弧分别相切于B点和C点.质量为Ⅲ的质点物块从A点由静止释放,恰好能到达D点,已知物块在圆弧AB上克服摩擦力做的功为Wl,在圆弧CD上克服摩擦力做的功为W2,重力加速度大小为g,则( )
如图所示,一固定竖直轨道由半径为R的四分之一圆弧AB、长度为L的水平直轨BC和半径为r的四分之一圆弧CD构成,BC与两网弧分别相切于B点和C点.质量为Ⅲ的质点物块从A点由静止释放,恰好能到达D点,已知物块在圆弧AB上克服摩擦力做的功为Wl,在圆弧CD上克服摩擦力做的功为W2,重力加速度大小为g,则( )
 如图所示,一固定竖直轨道由半径为R的四分之一圆弧AB、长度为L的水平直轨BC和半径为r的四分之一圆弧CD构成,BC与两网弧分别相切于B点和C点.质量为Ⅲ的质点物块从A点由静止释放,恰好能到达D点,已知物块在圆弧AB上克服摩擦力做的功为Wl,在圆弧CD上克服摩擦力做的功为W2,重力加速度大小为g,则( )
如图所示,一固定竖直轨道由半径为R的四分之一圆弧AB、长度为L的水平直轨BC和半径为r的四分之一圆弧CD构成,BC与两网弧分别相切于B点和C点.质量为Ⅲ的质点物块从A点由静止释放,恰好能到达D点,已知物块在圆弧AB上克服摩擦力做的功为Wl,在圆弧CD上克服摩擦力做的功为W2,重力加速度大小为g,则( )| A. | 物块在水平直轨上的动摩擦因数为$\frac{R+r}{L}$-$\frac{{W}_{1}+{W}_{2}}{mgL}$ | |
| B. | 物块在水平直轨上的动摩擦因数为$\frac{R-r}{L}$-$\frac{{W}_{1}+{W}_{2}}{mgL}$ | |
| C. | 物块在C点的向心加速度的大小为2g+$\frac{{2W}_{2}}{mr}$ | |
| D. | 物块在C点的向心加速度的大小为2g+$\frac{2({W}_{1}+{W}_{2})}{mr}$ |
 图示为一高山滑雪的运动场景,一质量m=65kg的滑雪爱好者,以v0=1m/s的初速度沿山坡匀加速滑下,山坡倾角θ=37°,在t=6s时间内滑下的路程s=42m.已知sin37°=0.6,cos37°=0.8,g取10m/s2,求滑雪者受到的阻力(包括摩擦力和空气阻力).
图示为一高山滑雪的运动场景,一质量m=65kg的滑雪爱好者,以v0=1m/s的初速度沿山坡匀加速滑下,山坡倾角θ=37°,在t=6s时间内滑下的路程s=42m.已知sin37°=0.6,cos37°=0.8,g取10m/s2,求滑雪者受到的阻力(包括摩擦力和空气阻力).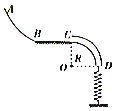 如图所示,水平地面BC与光滑曲面AB相切于B点,与内壁光滑的$\frac{1}{4}$细圆管CD相切于C点,管口D正下方直立一劲度系数为k的轻弹簧,弹簧下端固定,上端恰好与管口D齐平.将质量为m的小物块(可视为质点)放在弹簧上端且缓慢下压弹簧,当弹簧压缩的长度x1=$\frac{4mg}{k}$(其中g为重力加速度大小),对应弹簧的弹性势能Ep1=$\frac{8{m}^{2}{g}^{2}}{k}$时,由静止开始释放物块,物块进入管口D后沿DCBA轨道运动且不脱离轨道.已知物块速度最大时弹性势能Ep2=$\frac{{m}^{2}{g}^{2}}{2k}$,物块与BC间的动摩擦因数μ=0.8,BC的长度L1=$\frac{mg}{k}$,圆管CD的半径R=$\frac{mg}{k}$,求:
如图所示,水平地面BC与光滑曲面AB相切于B点,与内壁光滑的$\frac{1}{4}$细圆管CD相切于C点,管口D正下方直立一劲度系数为k的轻弹簧,弹簧下端固定,上端恰好与管口D齐平.将质量为m的小物块(可视为质点)放在弹簧上端且缓慢下压弹簧,当弹簧压缩的长度x1=$\frac{4mg}{k}$(其中g为重力加速度大小),对应弹簧的弹性势能Ep1=$\frac{8{m}^{2}{g}^{2}}{k}$时,由静止开始释放物块,物块进入管口D后沿DCBA轨道运动且不脱离轨道.已知物块速度最大时弹性势能Ep2=$\frac{{m}^{2}{g}^{2}}{2k}$,物块与BC间的动摩擦因数μ=0.8,BC的长度L1=$\frac{mg}{k}$,圆管CD的半径R=$\frac{mg}{k}$,求: 如图所示,固定的竖直光滑圆孤轨道的半径R=1.25m,A点与圆心O在同一水平线上,圆孤轨道底端B点与圆心在同一竖直线上,水平传送带以v0=4.0m/s的速度逆时针匀速运转,质量为0.5kg的物块从轨道上的A点由静止释放.已知传送带长度为L=3.0m,物块与传送带间的动摩擦因数μ=0.5,不计物块通过轨道与传送带交接处的动能损失,取g=10m/s2,试求:
如图所示,固定的竖直光滑圆孤轨道的半径R=1.25m,A点与圆心O在同一水平线上,圆孤轨道底端B点与圆心在同一竖直线上,水平传送带以v0=4.0m/s的速度逆时针匀速运转,质量为0.5kg的物块从轨道上的A点由静止释放.已知传送带长度为L=3.0m,物块与传送带间的动摩擦因数μ=0.5,不计物块通过轨道与传送带交接处的动能损失,取g=10m/s2,试求: