题目内容
16.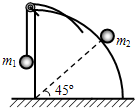 如图所示,光滑水平面上,有一$\frac{1}{4}$的球体,球体的左侧面也光滑.质量分别为m1、m2的物体(均可看作质点),通过柔软光滑的轻绳连接,与球体一起以共同的速度v0向左匀速运动,此时m2与球心O的连线与水平线成45°.m2与球面间的动摩擦因数为0.5,设m2与球面间的最大静摩擦力等于滑动摩擦力,则$\frac{m_2}{m_1}$的最小值是( )
如图所示,光滑水平面上,有一$\frac{1}{4}$的球体,球体的左侧面也光滑.质量分别为m1、m2的物体(均可看作质点),通过柔软光滑的轻绳连接,与球体一起以共同的速度v0向左匀速运动,此时m2与球心O的连线与水平线成45°.m2与球面间的动摩擦因数为0.5,设m2与球面间的最大静摩擦力等于滑动摩擦力,则$\frac{m_2}{m_1}$的最小值是( )| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | 2 | D. | $\sqrt{2}$ |
分析 对m1进行受力分析,受重力、支持力、拉力以及摩擦力处于平衡,当m1有最小值时,摩擦力沿球面向下.根据共点力平衡求出$\frac{{m}_{2}}{{m}_{1}}$的最小值.
解答 解:解:当m1有最大值时,摩擦力沿球面向下,受力如图
根据共点力平衡得,m2gsin45°+fm=T
fm=μN=μm2gcos45°
T=m1g
联立三式解得:$\frac{{m}_{2}}{{m}_{1}}$=$\frac{2\sqrt{2}}{3}$.
故选:B.
点评 解决本题的关键知道m1受到的最大静摩擦力可能沿球面向上,也可能沿球面向下,当沿球面向下时,m1有最小值.根据共点力平衡可得出质量比的最小值.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
7. 如图,有一轻圆环和插栓,在甲、乙、丙三个力作用下平衡时,圆环紧靠着插栓.不计圆环与插栓间的摩擦,若只调整两个力的大小,欲移动圆环使插栓位于圆环中心,下列说法正确的是( )
如图,有一轻圆环和插栓,在甲、乙、丙三个力作用下平衡时,圆环紧靠着插栓.不计圆环与插栓间的摩擦,若只调整两个力的大小,欲移动圆环使插栓位于圆环中心,下列说法正确的是( )
 如图,有一轻圆环和插栓,在甲、乙、丙三个力作用下平衡时,圆环紧靠着插栓.不计圆环与插栓间的摩擦,若只调整两个力的大小,欲移动圆环使插栓位于圆环中心,下列说法正确的是( )
如图,有一轻圆环和插栓,在甲、乙、丙三个力作用下平衡时,圆环紧靠着插栓.不计圆环与插栓间的摩擦,若只调整两个力的大小,欲移动圆环使插栓位于圆环中心,下列说法正确的是( )| A. | 增大甲、乙两力,且甲力增加较多 | B. | 增加乙、丙两力,且乙力增加较多 | ||
| C. | 增加甲、丙两力,且甲力增加较多 | D. | 增加乙、丙两力,且丙力增加较多 |
11.气体在容积固定的密闭容器中并且温度升高时,下列说法正确的是( )
| A. | 气体分子的平均动能变大,压强增大 | |
| B. | 气体分子做布朗运动的平均速率变大 | |
| C. | 气体分子的平均势能变大,压强增大 | |
| D. | 气体分子间的距离变大,压强减小 |
1.下面物理量中不属于标量的是( )
| A. | 电流强度 | B. | 电场强度 | C. | 功 | D. | 磁通量 |
8.某质点的振动图象如图,则下列说法正确的是( )


| A. | 该质点振动的周期是2s | |
| B. | 在1~2s内质点做初速度为零的变加速运动 | |
| C. | 在1.5s和2.5s末,质点的速度相同,加速度相同 | |
| D. | 在2.5s和3.5s末,质点的位移相同,速度相同 |
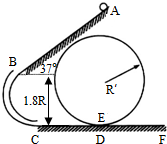 如图所示,倾斜轨道AB的倾角为37°,CD、EF轨道水平,AB与CD通过光滑圆弧管道BC连接,CD右端与竖直光滑圆周轨道相连.小球可以从D进入该轨道,沿轨道内侧运动,从E滑出该轨道进入EF水平轨道.小球由静止从A点释放,已知AB长为5R,CD长为R,重力加速度为g,小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5,sin37°=0.6,cos37°=0.8,圆弧管道BC入口B与出口C的高度差为1.8R.求:(在运算中,根号中的数值无需算出)
如图所示,倾斜轨道AB的倾角为37°,CD、EF轨道水平,AB与CD通过光滑圆弧管道BC连接,CD右端与竖直光滑圆周轨道相连.小球可以从D进入该轨道,沿轨道内侧运动,从E滑出该轨道进入EF水平轨道.小球由静止从A点释放,已知AB长为5R,CD长为R,重力加速度为g,小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5,sin37°=0.6,cos37°=0.8,圆弧管道BC入口B与出口C的高度差为1.8R.求:(在运算中,根号中的数值无需算出) 跳伞员常常采用“加速自由降落”(即AFF)的方法跳伞.如果一个质量为50kg的运动员在3658m的高度从飞机上跳出,自由降落40s时,竖直向下的速度达到50m/s,然后再打开降落伞(开伞时间不计),假设这一运动是匀加速直线运动.求:
跳伞员常常采用“加速自由降落”(即AFF)的方法跳伞.如果一个质量为50kg的运动员在3658m的高度从飞机上跳出,自由降落40s时,竖直向下的速度达到50m/s,然后再打开降落伞(开伞时间不计),假设这一运动是匀加速直线运动.求: 如图,水平放置的两条平行金属导轨MN和PQ上(导轨电阻不计),静止放着两条与导轨垂直的滑杆ad和bc,导轨间距为l,两滑杆距离为d.两滑杆的质量都是m,与导轨的动摩擦因数均为μ,两滑杆电阻均为R.空间有一匀强磁场垂直轨道平面向上,磁感应强度B=B0+kt(k>0).已知重力加速度为g.求:
如图,水平放置的两条平行金属导轨MN和PQ上(导轨电阻不计),静止放着两条与导轨垂直的滑杆ad和bc,导轨间距为l,两滑杆距离为d.两滑杆的质量都是m,与导轨的动摩擦因数均为μ,两滑杆电阻均为R.空间有一匀强磁场垂直轨道平面向上,磁感应强度B=B0+kt(k>0).已知重力加速度为g.求: 用水平力F=30N拉着一个质量为2kg的物体在水平面上由静止做匀加速直线运动,某时刻将力F随时间均匀减小.整个过程物体所受的摩擦力随时间变化如图中实线所示,求:
用水平力F=30N拉着一个质量为2kg的物体在水平面上由静止做匀加速直线运动,某时刻将力F随时间均匀减小.整个过程物体所受的摩擦力随时间变化如图中实线所示,求: