题目内容
19. 如图所示,在光滑水平面上有一质量为M的盒子,盒子中央有一质量为m的物体(可视为质点),它与盒底的动摩擦因数为μ,盒子内壁长l,现给物体以水平初速度v0向右运动,设物体与两壁碰撞是完全弹性碰撞.求物体m相对盒子静止前与盒壁碰撞的次数.
如图所示,在光滑水平面上有一质量为M的盒子,盒子中央有一质量为m的物体(可视为质点),它与盒底的动摩擦因数为μ,盒子内壁长l,现给物体以水平初速度v0向右运动,设物体与两壁碰撞是完全弹性碰撞.求物体m相对盒子静止前与盒壁碰撞的次数.
分析 物体在整个运动过程中,物体与盒子组成的系统动量守恒,由动量守恒定律求出物体m相对盒子静止时的共同速度.再根据能量守恒定律求得物体相对于盒子运动的距离,从而确定与盒子的碰撞次数.
解答 解:设物体与盒子相对静止时的共同速度为v,物体相对于盒子运动的总路程为s,以水平向右为正方向,根据动量守恒定律有:
mv0=(M+m)v
此过程中,根据能量守恒定律得:
$\frac{1}{2}$mv02=$\frac{1}{2}$(m+M)v2+μmgs
物体m相对盒子静止前与盒壁碰撞的次数为:n=$\frac{s-\frac{l}{2}}{l}$+1
解得:n=$\frac{1}{2}$+$\frac{M{v}_{0}^{2}}{2μ(M+m)gl}$
答:物体m相对盒子静止前与盒壁碰撞的次数是$\frac{1}{2}$+$\frac{M{v}_{0}^{2}}{2μ(M+m)gl}$.
点评 本题关键是根据动量守恒定律、能量守恒定律列式求解,要求同学们能正确分析物体和盒子的受力情况和运动情况,知道摩擦生热与相对路程有关,注意应用动量守恒定律解题时要规定正方向.

练习册系列答案
相关题目
9.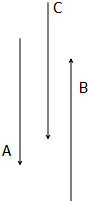 空间有两平行的长直导线A、B,其中导线A中的电流为I,导线B中的电流为2I,其电流方向如图所示,经测量可得导线A所受的安培力大小为F,如果在空间平行地放置另一通电长直导线C,且三条导线正好是一正三棱柱的三条棱,经测量可得导线A所受的安培力大小仍为F,下列说法正确的是( )
空间有两平行的长直导线A、B,其中导线A中的电流为I,导线B中的电流为2I,其电流方向如图所示,经测量可得导线A所受的安培力大小为F,如果在空间平行地放置另一通电长直导线C,且三条导线正好是一正三棱柱的三条棱,经测量可得导线A所受的安培力大小仍为F,下列说法正确的是( )
 空间有两平行的长直导线A、B,其中导线A中的电流为I,导线B中的电流为2I,其电流方向如图所示,经测量可得导线A所受的安培力大小为F,如果在空间平行地放置另一通电长直导线C,且三条导线正好是一正三棱柱的三条棱,经测量可得导线A所受的安培力大小仍为F,下列说法正确的是( )
空间有两平行的长直导线A、B,其中导线A中的电流为I,导线B中的电流为2I,其电流方向如图所示,经测量可得导线A所受的安培力大小为F,如果在空间平行地放置另一通电长直导线C,且三条导线正好是一正三棱柱的三条棱,经测量可得导线A所受的安培力大小仍为F,下列说法正确的是( )| A. | 导线B所受的安培力大小为$\sqrt{2}$F | B. | 导线B所受的安培力大小为$\sqrt{7}$F | ||
| C. | 导线C所受的安培力大小为F | D. | 导线C所受的安培力大小为$\sqrt{2}$F |
1. 如图,S1、S2是振幅均为A的两个水波波源,某时刻它们形成的波峰和波谷分别由实线和虚线表示.则( )
如图,S1、S2是振幅均为A的两个水波波源,某时刻它们形成的波峰和波谷分别由实线和虚线表示.则( )
 如图,S1、S2是振幅均为A的两个水波波源,某时刻它们形成的波峰和波谷分别由实线和虚线表示.则( )
如图,S1、S2是振幅均为A的两个水波波源,某时刻它们形成的波峰和波谷分别由实线和虚线表示.则( )| A. | 两列波在相遇区域发生干涉 | |
| B. | a处质点振动始终减弱,b、c处质点振动始终加强 | |
| C. | 此时a、b、c处各质点的位移是:xa=0,xb=-2A,xc=2A | |
| D. | a、b、c处各质点随着水波飘向远处 |
2.对于一定质量的理想气体,下列说法正确的是( )
| A. | 如果保持气体的体积不变,温度升高,压强减小 | |
| B. | 如果保持气体的体积不变,温度升高,压强增大 | |
| C. | 如果保持气体的温度不变,体积越小,压强越大 | |
| D. | 如果保持气体的压强不变,温度越高,体积越小 |
 如图所示,一个半径为R、内侧光滑的圆形轨道平放于光滑水平面上并被固定,其圆心为O.有a、b两个可视为质点的小球,分别静止靠在轨道内侧、直径AB的两端,两球质量分别为ma=4m和mb=m.现给a球一个沿轨道切线方向的水平初速度v0,使其从A向B运动并与b球发生弹性碰撞,已知两球碰撞时间极短,求两球第一次碰撞和第二次碰撞之间的时间间隔.
如图所示,一个半径为R、内侧光滑的圆形轨道平放于光滑水平面上并被固定,其圆心为O.有a、b两个可视为质点的小球,分别静止靠在轨道内侧、直径AB的两端,两球质量分别为ma=4m和mb=m.现给a球一个沿轨道切线方向的水平初速度v0,使其从A向B运动并与b球发生弹性碰撞,已知两球碰撞时间极短,求两球第一次碰撞和第二次碰撞之间的时间间隔.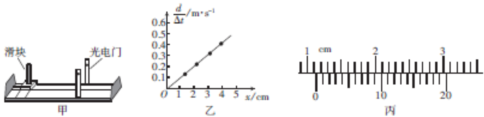

 如图所示,质量m=0.2kg的小球从某高度处以初速度v0=4m/s水平抛出,之后恰好沿着斜面方向落在倾角为37°的光滑斜面上,并沿着斜面下滑至地面,已知小球在斜面上下滑的时间为0.2s,不计空气阻力,取水平地面为重力势能的参考平面,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,质量m=0.2kg的小球从某高度处以初速度v0=4m/s水平抛出,之后恰好沿着斜面方向落在倾角为37°的光滑斜面上,并沿着斜面下滑至地面,已知小球在斜面上下滑的时间为0.2s,不计空气阻力,取水平地面为重力势能的参考平面,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,求: 如图,U型玻璃细管竖直放置,足够长水平细管又与U型玻璃细管底部相连通,各部分细管内径相同.水平细管内用小活塞封有长度为10cm的理想气体A,U型管左管上端封有长度为10cm的理想气体B,右管上端开口并与大气相通.此时U型玻璃管左右两侧水银面恰好相平,水银面距U型玻璃管底部的高度为15cm.现将活塞缓慢向左拉,使气体B的长度变为11cm.已知外界大气压强为75cmHg.求:
如图,U型玻璃细管竖直放置,足够长水平细管又与U型玻璃细管底部相连通,各部分细管内径相同.水平细管内用小活塞封有长度为10cm的理想气体A,U型管左管上端封有长度为10cm的理想气体B,右管上端开口并与大气相通.此时U型玻璃管左右两侧水银面恰好相平,水银面距U型玻璃管底部的高度为15cm.现将活塞缓慢向左拉,使气体B的长度变为11cm.已知外界大气压强为75cmHg.求: