题目内容
6. 城市中的路灯经常用三角形的结构悬挂,如图为这类结构的一种简化模型,图中硬杆OB可绕通过B点且垂直于纸面的轴转动,当选挂的重物质量为100N时,整个装置处于静止状态,硬杆OB水平,钢索OA与OB的夹角θ=45°,钢索OA和硬杆OB的重量都可忽略不计.试求:钢索OA和硬杆OB多O点的作用力各是多大?
城市中的路灯经常用三角形的结构悬挂,如图为这类结构的一种简化模型,图中硬杆OB可绕通过B点且垂直于纸面的轴转动,当选挂的重物质量为100N时,整个装置处于静止状态,硬杆OB水平,钢索OA与OB的夹角θ=45°,钢索OA和硬杆OB的重量都可忽略不计.试求:钢索OA和硬杆OB多O点的作用力各是多大?
分析 对O点受力分析,受重力、钢索的拉力、杆的支持力,根据平衡条件求解支持力和拉力.
解答 解:对O点受力分析,如图所示:
根据共点力平衡条件,有:
${F}_{A}=\frac{G}{sin45°}=\sqrt{2}G=100\sqrt{2}N$
FB=Gtan45°=G=100N
答:钢索OA和硬杆OB多O点的作用力分别为100$\sqrt{2}$N、100N.
点评 本题是三力平衡问题,关键是受力分析后根据平衡条件列式求解,可以采用合成法、分解法、正交分解法求解,基础题目.

练习册系列答案
相关题目
16.做平抛运动的物体初速度大小为v0,末速度大小为v,则物体飞行的时间为( )
| A. | $\frac{v-{v}_{0}}{g}$ | B. | $\frac{\sqrt{{v}^{2}-{{v}_{0}}^{2}}}{g}$ | C. | $\frac{\sqrt{{v}^{2}-{{v}_{0}}^{2}}}{2g}$ | D. | $\frac{v}{g}$ |
14. 如图所示,重为G的物体静止在水平地面上,此时物体对地面的压力等于重力G,如果选择下列规律中的某个中几个作为依据来证明 上述结论,最为合适的一项是( )
如图所示,重为G的物体静止在水平地面上,此时物体对地面的压力等于重力G,如果选择下列规律中的某个中几个作为依据来证明 上述结论,最为合适的一项是( )
①牛顿第一定律 ②牛顿第二定律 ③牛顿第三定律.
 如图所示,重为G的物体静止在水平地面上,此时物体对地面的压力等于重力G,如果选择下列规律中的某个中几个作为依据来证明 上述结论,最为合适的一项是( )
如图所示,重为G的物体静止在水平地面上,此时物体对地面的压力等于重力G,如果选择下列规律中的某个中几个作为依据来证明 上述结论,最为合适的一项是( )①牛顿第一定律 ②牛顿第二定律 ③牛顿第三定律.
| A. | ① | B. | ①② | C. | ③ | D. | ②③ |
4. 如图所示,在倾角为θ的U形金属导轨上放置一根导电棒MN,开始时导电棒MN处于静止状态.今在导轨所在空间加一个垂直于导轨平面斜向下的,逐渐增大的磁场,使感应电流逐渐增大,经过时间t导电棒开始运动,那么在这段时间t内,导电棒受到的摩擦力的大小( )
如图所示,在倾角为θ的U形金属导轨上放置一根导电棒MN,开始时导电棒MN处于静止状态.今在导轨所在空间加一个垂直于导轨平面斜向下的,逐渐增大的磁场,使感应电流逐渐增大,经过时间t导电棒开始运动,那么在这段时间t内,导电棒受到的摩擦力的大小( )
 如图所示,在倾角为θ的U形金属导轨上放置一根导电棒MN,开始时导电棒MN处于静止状态.今在导轨所在空间加一个垂直于导轨平面斜向下的,逐渐增大的磁场,使感应电流逐渐增大,经过时间t导电棒开始运动,那么在这段时间t内,导电棒受到的摩擦力的大小( )
如图所示,在倾角为θ的U形金属导轨上放置一根导电棒MN,开始时导电棒MN处于静止状态.今在导轨所在空间加一个垂直于导轨平面斜向下的,逐渐增大的磁场,使感应电流逐渐增大,经过时间t导电棒开始运动,那么在这段时间t内,导电棒受到的摩擦力的大小( )| A. | 不断增加 | B. | 不断减少 | C. | 先增大后减少 | D. | 先减少后增大 |
11. 如图所示,AB、CD是一个圆的两条直径,该圆处于匀强电场中,电场强度方向平行该圆所在平面,在圆周所在的平面内将一个带正电的粒子从A点以相同的速率沿不同方向射向圆形区域,粒子将经过圆周上的不同点,其中经过C点时粒子的动能最小.若不计粒子所受的重力和空气阻力,则下列判断中正确的是( )
如图所示,AB、CD是一个圆的两条直径,该圆处于匀强电场中,电场强度方向平行该圆所在平面,在圆周所在的平面内将一个带正电的粒子从A点以相同的速率沿不同方向射向圆形区域,粒子将经过圆周上的不同点,其中经过C点时粒子的动能最小.若不计粒子所受的重力和空气阻力,则下列判断中正确的是( )
 如图所示,AB、CD是一个圆的两条直径,该圆处于匀强电场中,电场强度方向平行该圆所在平面,在圆周所在的平面内将一个带正电的粒子从A点以相同的速率沿不同方向射向圆形区域,粒子将经过圆周上的不同点,其中经过C点时粒子的动能最小.若不计粒子所受的重力和空气阻力,则下列判断中正确的是( )
如图所示,AB、CD是一个圆的两条直径,该圆处于匀强电场中,电场强度方向平行该圆所在平面,在圆周所在的平面内将一个带正电的粒子从A点以相同的速率沿不同方向射向圆形区域,粒子将经过圆周上的不同点,其中经过C点时粒子的动能最小.若不计粒子所受的重力和空气阻力,则下列判断中正确的是( )| A. | 电场强度方向由A指向B | B. | 电场强度方向由C指向D | ||
| C. | 粒子到达B点时动能最大 | D. | 粒子到达D点时电势能最小 |
8.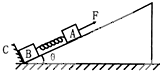 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
 在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态.现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A沿斜面运动的距离为d,速度为v,此时( )| A. | 拉力F做功的等于A动能的增加量 | |
| B. | 物块B满足m2gsinθ=kd | |
| C. | 物块A的加速度为$\frac{F-kd}{{m}_{1}}$ | |
| D. | 弹簧弹性势能的增加量为Fd-m1gdsinθ-$\frac{1}{2}$m1v2 |
9. 真空中三维坐标系Oxyz的z轴方向竖直向上,在坐标原点0上固定一带正电的点电荷Q,其形成的电场如图所示,一重力不能忽略的带电微粒q正在该点电荷附近做匀速圆周运动.则( )
真空中三维坐标系Oxyz的z轴方向竖直向上,在坐标原点0上固定一带正电的点电荷Q,其形成的电场如图所示,一重力不能忽略的带电微粒q正在该点电荷附近做匀速圆周运动.则( )
 真空中三维坐标系Oxyz的z轴方向竖直向上,在坐标原点0上固定一带正电的点电荷Q,其形成的电场如图所示,一重力不能忽略的带电微粒q正在该点电荷附近做匀速圆周运动.则( )
真空中三维坐标系Oxyz的z轴方向竖直向上,在坐标原点0上固定一带正电的点电荷Q,其形成的电场如图所示,一重力不能忽略的带电微粒q正在该点电荷附近做匀速圆周运动.则( )| A. | 该微粒带负电,轨道圆心在坐标原点O上 | |
| B. | 该微粒带负电,轨道圆心在z轴的负半轴上某一点 | |
| C. | 该微粒带正电,轨道圆心在坐标原点0上 | |
| D. | 该微粒带正电,轨道圆心在z轴的正半轴上某一点 |
 如图所示,光滑的平行金属导轨电阻可忽略,两导轨间距离L=0.75m,导轨倾角α=30°,导轨上端接一阻值R=2.5Ω的电阻,整个装置处于垂直轨道平面平面向上的匀强磁场中.阻值r=0.5Ω,质量m=0.2kg的金属棒与轨道垂直且接触良好,其从轨上端.ab处由静止开始下滑,当金属棒沿导轨下滑距离s=1.2m时,速度达到最大值vm=3m/s,重力加速度g=10m/s2,求:
如图所示,光滑的平行金属导轨电阻可忽略,两导轨间距离L=0.75m,导轨倾角α=30°,导轨上端接一阻值R=2.5Ω的电阻,整个装置处于垂直轨道平面平面向上的匀强磁场中.阻值r=0.5Ω,质量m=0.2kg的金属棒与轨道垂直且接触良好,其从轨上端.ab处由静止开始下滑,当金属棒沿导轨下滑距离s=1.2m时,速度达到最大值vm=3m/s,重力加速度g=10m/s2,求: 如图所示,水平传送带AB长2m,以v=1m/s的速度匀速运动,质量均为4kg的小物体P、Q与绕过定滑轮的轻绳相连,t=0时刻P、在传送带A端以初速度v0=4m/s向右运动,已知P与传送带间动摩擦因数为0.5,P在传动带上运动过程它与定滑轮间的绳始终水平,不计定滑轮质量和摩擦,绳不可伸长且足够长度,最大静摩擦力视为等于滑动摩擦力,取g=10m/s2,求:
如图所示,水平传送带AB长2m,以v=1m/s的速度匀速运动,质量均为4kg的小物体P、Q与绕过定滑轮的轻绳相连,t=0时刻P、在传送带A端以初速度v0=4m/s向右运动,已知P与传送带间动摩擦因数为0.5,P在传动带上运动过程它与定滑轮间的绳始终水平,不计定滑轮质量和摩擦,绳不可伸长且足够长度,最大静摩擦力视为等于滑动摩擦力,取g=10m/s2,求: