题目内容
18. 如图所示,一质量m=2kg的铁块放在种类M=2kg的小车左端,二者一起以v0=4m/s的速度沿光滑水平面向竖直墙运动,车与墙碰撞的时间t=0.01s,不计碰撞时机械能的损失.铁块与小车之间的动摩擦因数μ=0.2,铁块不会到达车的右端,最终小车与铁块相对静止.求:
如图所示,一质量m=2kg的铁块放在种类M=2kg的小车左端,二者一起以v0=4m/s的速度沿光滑水平面向竖直墙运动,车与墙碰撞的时间t=0.01s,不计碰撞时机械能的损失.铁块与小车之间的动摩擦因数μ=0.2,铁块不会到达车的右端,最终小车与铁块相对静止.求:①车与墙碰撞的平均作用力的大小F;
②小车车长的最小值.
分析 ①车与墙碰撞过程,根据动量定理列式求解平均作用力;
②对车和铁块组成的系统为研究对象,系统所受的合力为零,动量守恒,即可求出小车与铁块共同运动的速度,再根据能量守恒定律求出小车的最小长度.
解答 解:①车与墙碰撞过程中,不计碰撞时机械能的损失,则车与墙碰撞后的瞬间,小车的速度向左,大小为v0,设向左为正,
根据动量定理得:
Ft=Mv0-M(-v0)
解得:F=$\frac{2×2×4}{0.01}$=1600N
②对车和铁块组成的系统为研究对象,系统所受的合力为零.
以向左为正方向,由动量守恒定律得:Mv0-mv0=(M+m)v,
解得:v=0,
对系统,由能量守恒定律得:$\frac{1}{2}$(M+m)v02=μmgL,
解得:L=8m
答:①车与墙碰撞的平均作用力的大小F为1600N.
②小车车长的最小值为8m
点评 本题涉及到两个物体的相互作用,应优先考虑动量守恒定律.运用动量守恒定律研究物体的速度,比牛顿第二定律和运动学公式结合简单,因为动量守恒定律不涉及运动的细节和过程.涉及时间问题,可优先考虑动量定理.

练习册系列答案
相关题目
9. 如图所示,现用水平外力将一个矩形导体线框两次从图示位置以一定的速度匀速拉出磁场,第一次速度为v,第二次速度为2v,下列说法正确的是( )
如图所示,现用水平外力将一个矩形导体线框两次从图示位置以一定的速度匀速拉出磁场,第一次速度为v,第二次速度为2v,下列说法正确的是( )
 如图所示,现用水平外力将一个矩形导体线框两次从图示位置以一定的速度匀速拉出磁场,第一次速度为v,第二次速度为2v,下列说法正确的是( )
如图所示,现用水平外力将一个矩形导体线框两次从图示位置以一定的速度匀速拉出磁场,第一次速度为v,第二次速度为2v,下列说法正确的是( )| A. | 线框中的感应电流方向是逆时针 | B. | 两次线框中的感应电流之比为1:2 | ||
| C. | 两次作用在线框上的外力之比1:2 | D. | 两次线框中产生的热量之比为1:4 |
6. 如图为一列简谐横波某时刻的波形图,介质中有P、Q、M三个质点,此时的纵坐标分别为yP=2cm,yQ=-2cm.下列说法正确的是( )
如图为一列简谐横波某时刻的波形图,介质中有P、Q、M三个质点,此时的纵坐标分别为yP=2cm,yQ=-2cm.下列说法正确的是( )
 如图为一列简谐横波某时刻的波形图,介质中有P、Q、M三个质点,此时的纵坐标分别为yP=2cm,yQ=-2cm.下列说法正确的是( )
如图为一列简谐横波某时刻的波形图,介质中有P、Q、M三个质点,此时的纵坐标分别为yP=2cm,yQ=-2cm.下列说法正确的是( )| A. | P、Q两质点的速度方向总是相同 | |
| B. | Q、M两质点的加速度总是相同 | |
| C. | P、M两质点的速度总是大小相等、方向相反 | |
| D. | 在任何相等时间内,P、M两质点通过的路程总相等 | |
| E. | P、M两质点对平衡位置的位移总是大小相等、方向相反 |
10.图(甲)是线圈P绕垂直于磁场的轴在匀强磁场中匀速转动时所产生的正弦式交变电压的图象,把该电压加在如图(乙)所示的理想变压器的A、B端,已知电压表的示数为4.0V,图中的电压表和电流表均为理想电表,R=2Ω,其它电阻不计.下列说法中正确的是( )


| A. | 电流表的示数为0.8A | |
| B. | 当t=0.2s和0.4s时,穿过线圈P的磁通量最小 | |
| C. | 线圈P的转速为300r/min | |
| D. | 变压器原线圈Ⅰ和副线圈Ⅱ的匝数比为2:5 |
 质量为0.2kg的弹性小球从空中某处静止下落,下落过程中对应的v-t图象如图所示,经过0.5s小球与水平地面相碰后反弹,反弹速度大小变为碰撞前的$\frac{3}{4}$,设小球运动中所受的空气阻力大小不变,g=10m/s2,求:
质量为0.2kg的弹性小球从空中某处静止下落,下落过程中对应的v-t图象如图所示,经过0.5s小球与水平地面相碰后反弹,反弹速度大小变为碰撞前的$\frac{3}{4}$,设小球运动中所受的空气阻力大小不变,g=10m/s2,求: 如图甲所示.直角坐标系xOy中,第二象限内有沿x轴正方向的匀强磁场,第一四象限内有垂直坐标平面的匀强交变磁场,磁场方向以垂直纸面向外为正方向.第三象限内有一发射装置(没有画出)沿y轴正方向射出一个比荷$\frac{q}{m}$=100C/kg的带正电的粒子(可视为质点且不计重力),该粒子以v0=10m/s的速度从x轴上的点A(-1m,0)进入第二象限,从y轴上的C点(0,2m)进入第一象限,取粒子刚进入第一象限的时刻为0时刻,第一、四象限内磁场的磁感应强度按图乙所示规律变化,求:
如图甲所示.直角坐标系xOy中,第二象限内有沿x轴正方向的匀强磁场,第一四象限内有垂直坐标平面的匀强交变磁场,磁场方向以垂直纸面向外为正方向.第三象限内有一发射装置(没有画出)沿y轴正方向射出一个比荷$\frac{q}{m}$=100C/kg的带正电的粒子(可视为质点且不计重力),该粒子以v0=10m/s的速度从x轴上的点A(-1m,0)进入第二象限,从y轴上的C点(0,2m)进入第一象限,取粒子刚进入第一象限的时刻为0时刻,第一、四象限内磁场的磁感应强度按图乙所示规律变化,求:



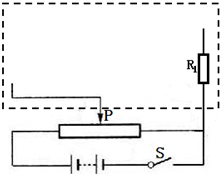 现有一电流表
现有一电流表 ,量程30mA,内阻r1约为6欧,请用下列器材测量其内阻值r1,要求方法简捷,有尽可能高的测量精度.
,量程30mA,内阻r1约为6欧,请用下列器材测量其内阻值r1,要求方法简捷,有尽可能高的测量精度. ,量程50mA,内电阻r2约10Ω
,量程50mA,内电阻r2约10Ω ,量程15V,内阻rV=15kΩ
,量程15V,内阻rV=15kΩ 内电阻的计算表达式r1=$\frac{({I}_{2}-{I}_{1}){R}_{0}^{\;}}{{I}_{1}}$(用相应的物理量符号表示).
内电阻的计算表达式r1=$\frac{({I}_{2}-{I}_{1}){R}_{0}^{\;}}{{I}_{1}}$(用相应的物理量符号表示). 如图所示,光滑绝缘杆竖直放置,它与以正点电荷Q为圆心的某一圆周交于B、C两点,质量为m、带电荷量为-q的有孔小球从杆上的A点无初速度下滑,已知q?Q,AB=h,小球滑到B点时速度大小为$\sqrt{5gh}$,则小球从A运动到B的过程中,电场力做多少功?若取A点电势为零,C点电势是多大?
如图所示,光滑绝缘杆竖直放置,它与以正点电荷Q为圆心的某一圆周交于B、C两点,质量为m、带电荷量为-q的有孔小球从杆上的A点无初速度下滑,已知q?Q,AB=h,小球滑到B点时速度大小为$\sqrt{5gh}$,则小球从A运动到B的过程中,电场力做多少功?若取A点电势为零,C点电势是多大?