题目内容
4.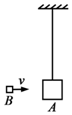 如图,物块A通过一不可伸长的轻绳悬挂在天花板下,初始时静止.从发射器(图中未画出)射出的物块B沿水平方向与A相撞,碰撞前B的速度大小为v,碰撞后两者粘连在一起运动.已知A和B的质量分别M和m,重力加速度大小为g,不计空气阻力,求:
如图,物块A通过一不可伸长的轻绳悬挂在天花板下,初始时静止.从发射器(图中未画出)射出的物块B沿水平方向与A相撞,碰撞前B的速度大小为v,碰撞后两者粘连在一起运动.已知A和B的质量分别M和m,重力加速度大小为g,不计空气阻力,求:(1)碰撞后A、B的共同速度v′的大小;
(2)碰撞后A、B一起上升的最大高度h.
分析 (1)物块B与A碰撞过程,系统的动量定律,由动量守恒定律求碰撞后A、B的共同速度v′的大小;
(2)碰撞后A、B一起上升的过程中,只有重力做功,其机械能守恒,由机械能守恒定律求最大高度h.
解答 解:(1)物块B与A碰撞过程,取水平向右为正方向,对A、B组成的系统,由动量守恒定律得:
mv=(m+M)v'
解得:v'=$\frac{mv}{m+M}$
(2)A、B碰后一起向上运动的过程,由机械能守恒得
$\frac{1}{2}(M+m){v}^{2}$=(M+m)gh
联立解得:h=$\frac{{m}^{2}{v}^{2}}{2g(M+m)^{2}}$
答:
(1)碰撞后A、B的共同速度v′的大小为$\frac{mv}{m+M}$;
(2)碰撞后A、B一起上升的最大高度h为$\frac{{m}^{2}{v}^{2}}{2g(M+m)^{2}}$.
点评 解决本题时要理清物块的运动过程,知道碰撞的基本规律是动量守恒定律,运用动量守恒定律时要选择正方向.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
12. 如图所示,高为h的光滑斜面体abc固定在水平地面上,其中a、b分别为斜面的顶端与低端,将一质量为m的小球从a点由静止释放,取地面为零势能面,重力加速度其g,一下说法正确的是( )
如图所示,高为h的光滑斜面体abc固定在水平地面上,其中a、b分别为斜面的顶端与低端,将一质量为m的小球从a点由静止释放,取地面为零势能面,重力加速度其g,一下说法正确的是( )
 如图所示,高为h的光滑斜面体abc固定在水平地面上,其中a、b分别为斜面的顶端与低端,将一质量为m的小球从a点由静止释放,取地面为零势能面,重力加速度其g,一下说法正确的是( )
如图所示,高为h的光滑斜面体abc固定在水平地面上,其中a、b分别为斜面的顶端与低端,将一质量为m的小球从a点由静止释放,取地面为零势能面,重力加速度其g,一下说法正确的是( )| A. | 小球在a点时的重力势能为mgh | B. | 小球在b点时的重力势能为mgh | ||
| C. | 小球在a点时的机械能为mgh | D. | 小球在b点时的机械能为mgh |
19.下列现象中,属于光的色散现象的是( )
| A. | 雨后天空出现彩虹 | |
| B. | 通过一个狭缝观察日光灯可看到彩色条纹 | |
| C. | 海市蜃楼现象 | |
| D. | 日光照射在肥皂泡上出现彩色条纹 |
9. 如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角2θ.当小球以某一角速度匀速转动时,恰好对锥面无压力,则下列说法正确的是( )
如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角2θ.当小球以某一角速度匀速转动时,恰好对锥面无压力,则下列说法正确的是( )
 如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角2θ.当小球以某一角速度匀速转动时,恰好对锥面无压力,则下列说法正确的是( )
如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角2θ.当小球以某一角速度匀速转动时,恰好对锥面无压力,则下列说法正确的是( )| A. | 小球运动的角速度大小是$\sqrt{\frac{g}{Lcosθ}}$ | B. | 小球运动的角速度大小是$\sqrt{\frac{gtanθ}{L}}$ | ||
| C. | 细线的拉力大小是$\frac{mg}{sinθ}$ | D. | 细线的拉力大小是$\frac{mg}{cosθ}$ |
16.关于机械能,以下说法正确的是( )
| A. | 质量大的物体,重力势能一定大 | |
| B. | 速度大的物体,动能一定大 | |
| C. | 做平抛运动的物体机械能时刻在变化 | |
| D. | 质量和速率都相同的物体,动能一定相同 |
11. 如图甲所示,导体棒MN置于水平导轨上,PQMN所围的成面积为S,PQ之间有阻值为R的电阻,不计导轨和导体棒的电阻.导轨所在区域内存在沿竖直方向的匀强磁场,规定磁场方向竖直向上为正,在0~2t0时间内磁感应强度的变化情况如图乙所示,导体棒MN始终处于静止状态.下列说法正确的是( )
如图甲所示,导体棒MN置于水平导轨上,PQMN所围的成面积为S,PQ之间有阻值为R的电阻,不计导轨和导体棒的电阻.导轨所在区域内存在沿竖直方向的匀强磁场,规定磁场方向竖直向上为正,在0~2t0时间内磁感应强度的变化情况如图乙所示,导体棒MN始终处于静止状态.下列说法正确的是( )
 如图甲所示,导体棒MN置于水平导轨上,PQMN所围的成面积为S,PQ之间有阻值为R的电阻,不计导轨和导体棒的电阻.导轨所在区域内存在沿竖直方向的匀强磁场,规定磁场方向竖直向上为正,在0~2t0时间内磁感应强度的变化情况如图乙所示,导体棒MN始终处于静止状态.下列说法正确的是( )
如图甲所示,导体棒MN置于水平导轨上,PQMN所围的成面积为S,PQ之间有阻值为R的电阻,不计导轨和导体棒的电阻.导轨所在区域内存在沿竖直方向的匀强磁场,规定磁场方向竖直向上为正,在0~2t0时间内磁感应强度的变化情况如图乙所示,导体棒MN始终处于静止状态.下列说法正确的是( )| A. | 在0~2t0时间内,导轨棒受到的导轨的摩擦力方向先向左后向右,大小不变 | |
| B. | 在0~t0内,通过导体棒的电流方向为N到M | |
| C. | 在t0~2t0内,通过电阻R的电流大小为$\frac{S{B}_{0}}{R{t}_{0}}$ | |
| D. | 在0~2t0时间内,通过电阻R的电荷量为$\frac{S{B}_{0}}{2R}$ |
 如图所示,一轻弹簧原长为2R,其一端固定在倾角为370的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然状态,直轨道与一半径为$\frac{5}{6}$R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直平面内.质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高到达F点,AF=4R,已知P与直轨道间的动摩擦因数?=$\frac{1}{4}$,重力加速度为g,sin37°=0.6,cos37°=0.8.则:
如图所示,一轻弹簧原长为2R,其一端固定在倾角为370的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然状态,直轨道与一半径为$\frac{5}{6}$R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直平面内.质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高到达F点,AF=4R,已知P与直轨道间的动摩擦因数?=$\frac{1}{4}$,重力加速度为g,sin37°=0.6,cos37°=0.8.则: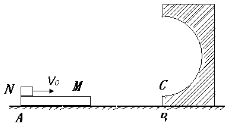 如图所示,质量为1Kg的小滑块N(可视为质点)放在质量也为1Kg的长木板M左端,N和M之间的动摩擦因数μ1=0.5,M和地面之间的动摩擦因数μ2=0.1,现给小滑块N一个水平向右的初速v0=8m/s,小滑块N和长木板M同时到达B点且此时速度大小恰好相等,小滑块到达长木板右端后,能够由C点平滑地滑上固定的光滑圆弧轨道,圆轨道半径R=0.3m,重力加速度g取10m/s2,求:
如图所示,质量为1Kg的小滑块N(可视为质点)放在质量也为1Kg的长木板M左端,N和M之间的动摩擦因数μ1=0.5,M和地面之间的动摩擦因数μ2=0.1,现给小滑块N一个水平向右的初速v0=8m/s,小滑块N和长木板M同时到达B点且此时速度大小恰好相等,小滑块到达长木板右端后,能够由C点平滑地滑上固定的光滑圆弧轨道,圆轨道半径R=0.3m,重力加速度g取10m/s2,求: