��Ŀ����
9�� ��ͼ��ʾ���ڹ⻬��Բ���ó�ΪL��ϸ������һ����Ϊm��С��Բ����2�ȣ���С����ijһ���ٶ�����ת��ʱ��ǡ�ö�����ѹ����������˵����ȷ���ǣ�������
��ͼ��ʾ���ڹ⻬��Բ���ó�ΪL��ϸ������һ����Ϊm��С��Բ����2�ȣ���С����ijһ���ٶ�����ת��ʱ��ǡ�ö�����ѹ����������˵����ȷ���ǣ�������| A�� | С���˶��Ľ��ٶȴ�С��$\sqrt{\frac{g}{Lcos��}}$ | B�� | С���˶��Ľ��ٶȴ�С��$\sqrt{\frac{gtan��}{L}}$ | ||
| C�� | ϸ�ߵ�������С��$\frac{mg}{sin��}$ | D�� | ϸ�ߵ�������С��$\frac{mg}{cos��}$ |
���� ��С����ijһ���ٶ�����ת��ʱ��ǡ�ö�����ѹ������С�����������������ӵ��������������ֽ⣬����ֱ������С������ƽ�⣬��ʽ��⼴�ɽ�����ӵ�����������������Ĺ�ʽ�ɽ�ô�ʱ�Ľ��ٶȣ�
��� �⣺��С����ijһ���ٶ�����ת��ʱ��ǡ�ö�����ѹ�������С���֧����Ϊ�㣬С���ܵ�����mg����������T�����ʱ���ٶ�Ϊ�أ�
����ţ�ٵڶ����ɵã�
Tsin��=m��2Lsin�� ��
Tcos��=mg�� ��
�ɢ٢���ʽ�ã�mgtan��=m��2Lsin��
����=$\sqrt{\frac{g}{Lcos��}}$
ϸ�ߵ�������С T=$\frac{mg}{cos��}$����AD��ȷ��BC����
��ѡ��AD
���� �������Ĺؼ�����ȷС����Բ���˶�ʱ����������Դ�����ţ�ٵڶ����ɽ�����⣬���úϳɷ��о���

��ϰ��ϵ�д�
�����Ŀ
19�� ����Ϊm��С��ϵ�����һ�ˣ�����ֱƽ�������뾶ΪR��Բ���˶����˶�������С���ܵ������������ã�ijʱ�̣�С��ͨ�������͵㣬��˶����������СΪ7mg���˺�С����Բ���˶����������ܵ�����ߵ�ʱ���˶������������СΪ$\frac{1}{2}$mg�������������С��˷��������������Ĺ������ǣ�������
����Ϊm��С��ϵ�����һ�ˣ�����ֱƽ�������뾶ΪR��Բ���˶����˶�������С���ܵ������������ã�ijʱ�̣�С��ͨ�������͵㣬��˶����������СΪ7mg���˺�С����Բ���˶����������ܵ�����ߵ�ʱ���˶������������СΪ$\frac{1}{2}$mg�������������С��˷��������������Ĺ������ǣ�������
 ����Ϊm��С��ϵ�����һ�ˣ�����ֱƽ�������뾶ΪR��Բ���˶����˶�������С���ܵ������������ã�ijʱ�̣�С��ͨ�������͵㣬��˶����������СΪ7mg���˺�С����Բ���˶����������ܵ�����ߵ�ʱ���˶������������СΪ$\frac{1}{2}$mg�������������С��˷��������������Ĺ������ǣ�������
����Ϊm��С��ϵ�����һ�ˣ�����ֱƽ�������뾶ΪR��Բ���˶����˶�������С���ܵ������������ã�ijʱ�̣�С��ͨ�������͵㣬��˶����������СΪ7mg���˺�С����Բ���˶����������ܵ�����ߵ�ʱ���˶������������СΪ$\frac{1}{2}$mg�������������С��˷��������������Ĺ������ǣ�������| A�� | $\frac{1}{4}$mgR | B�� | $\frac{1}{2}$mgR | C�� | $\frac{3}{4}$mgR | D�� | mgR |
20����һ�⻬ˮƽ���ڽ���ƽ��ֱ������ϵ��һ�����t=0ʱ����������ԭ��O��0��0����ʼ�˶�������x���y�᷽���˶����ٶ�-ʱ��ͼ����ͼ�ס�����ʾ������˵������ȷ���ǣ�������

| A�� | ǰ2s���������ȼ���ֱ���˶������ٶ���x�᷽�� | |
| B�� | ��2s������������ȼ���ֱ���˶��������ٶ���y�᷽�� | |
| C�� | 4s ĩ��������Ϊ��4 m��4 m�� | |
| D�� | 4 sĩ��������Ϊ��6m��2m�� |
17�����������ڷֱ�����һ���ǶȺ�ͬʱ�ͷţ�������г�˶����Ա������ڵ�������˵����ȷ���ǣ�������
| A�� | ��ֻ�ǰ���������ͬ��������������ڳ� | |
| B�� | ��ֻ�ǰ���������ͬ��������С�����ڳ� | |
| C�� | ��ֻ�ǰڳ���ͬ����ڳ��������ڳ� | |
| D�� | ��ֻ�ǰڳ���ͬ����ڳ��̵����ڳ� |
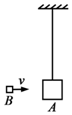 ��ͼ�����Aͨ��һ�����쳤�������������컨���£���ʼʱ��ֹ���ӷ�������ͼ��δ��������������B��ˮƽ������A��ײ����ײǰB���ٶȴ�СΪv����ײ������ճ����һ���˶�����֪A��B�������ֱ�M��m���������ٶȴ�СΪg�����ƿ�����������
��ͼ�����Aͨ��һ�����쳤�������������컨���£���ʼʱ��ֹ���ӷ�������ͼ��δ��������������B��ˮƽ������A��ײ����ײǰB���ٶȴ�СΪv����ײ������ճ����һ���˶�����֪A��B�������ֱ�M��m���������ٶȴ�СΪg�����ƿ�����������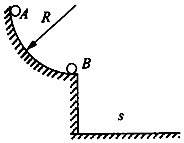 ��ͼ��ʾ��һ���뾶ΪR=1.00m��$\frac{1}{4}$�ֲ�Բ�¹�����̶�����ֱƽ���ڣ����¶�������ˮƽ�ģ�����¶˾����߶�Ϊh=1.25m�ڹ��ĩ�˷�������ΪmB=0.05kg��С����Ϊ�ʵ㣩��B�������װ���ʹ���������һ����ΪmA=0.10kg��С��A��Ҳ��Ϊ�ʵ㣩�ɹ���϶˵�Ӿ�ֹ��ʼ�ͷţ��˶��������ʹ�ʱ����������ʾ����Ϊ2.6N��A��B��������������BС��ˮƽ�ɳ����䵽����ʱ��ˮƽλ��Ϊs=1.00m�����ƿ����������������ٶ�ȡg=10m/s2����
��ͼ��ʾ��һ���뾶ΪR=1.00m��$\frac{1}{4}$�ֲ�Բ�¹�����̶�����ֱƽ���ڣ����¶�������ˮƽ�ģ�����¶˾����߶�Ϊh=1.25m�ڹ��ĩ�˷�������ΪmB=0.05kg��С����Ϊ�ʵ㣩��B�������װ���ʹ���������һ����ΪmA=0.10kg��С��A��Ҳ��Ϊ�ʵ㣩�ɹ���϶˵�Ӿ�ֹ��ʼ�ͷţ��˶��������ʹ�ʱ����������ʾ����Ϊ2.6N��A��B��������������BС��ˮƽ�ɳ����䵽����ʱ��ˮƽλ��Ϊs=1.00m�����ƿ����������������ٶ�ȡg=10m/s2����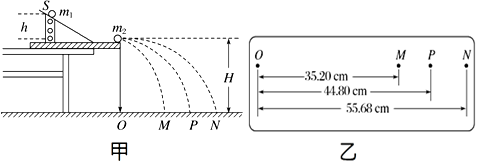
 ��ͼ��AB�dz���s=0.5m��ˮƽ�����B����뾶ΪR=0.1m�Ĺ⻬��Բ���BCD���У���Բ��ֱ��BD��ֱ��A�����̶�һ����Ǧ�=30��Ĺ⻬б�棬���Ӵ�˳�������������֣��㹻�ߣ����������˷ֱ�ϵ��С���a��b��a������m1=1kg����ʼʱ��b��ѹ�ڵ��治����aλ��б���ϸ�h=0.5m�ĵط�����ʱ������ߵ�������ֱ���ұߵ�����ͻȻ�Ͽ���a��������ˮƽ���˶���Ȼ���Ϲ��BCD����֪a�����Ķ�Ħ��������=0.2��gȡ10m/s2��
��ͼ��AB�dz���s=0.5m��ˮƽ�����B����뾶ΪR=0.1m�Ĺ⻬��Բ���BCD���У���Բ��ֱ��BD��ֱ��A�����̶�һ����Ǧ�=30��Ĺ⻬б�棬���Ӵ�˳�������������֣��㹻�ߣ����������˷ֱ�ϵ��С���a��b��a������m1=1kg����ʼʱ��b��ѹ�ڵ��治����aλ��б���ϸ�h=0.5m�ĵط�����ʱ������ߵ�������ֱ���ұߵ�����ͻȻ�Ͽ���a��������ˮƽ���˶���Ȼ���Ϲ��BCD����֪a�����Ķ�Ħ��������=0.2��gȡ10m/s2�� ��ͼ��ʾ��ABC��DEFΪͬһ��ֱƽ���ڵ������̶��⻬���������ABC��ĩ��ˮƽ��DEFΪֱ����ֱ����İ�Բ�ι����r=0.5m����һ����m=1kg�Ļ��飨����Ϊ�ʵ㣩�ӹ��ABC�ϵ�A���ɾ�ֹ�ͷţ������龭C���ǡ���ع��DEF��Բ���˶���gȡ10m/s2����
��ͼ��ʾ��ABC��DEFΪͬһ��ֱƽ���ڵ������̶��⻬���������ABC��ĩ��ˮƽ��DEFΪֱ����ֱ����İ�Բ�ι����r=0.5m����һ����m=1kg�Ļ��飨����Ϊ�ʵ㣩�ӹ��ABC�ϵ�A���ɾ�ֹ�ͷţ������龭C���ǡ���ع��DEF��Բ���˶���gȡ10m/s2����