题目内容
6. 质量为m的均匀木块静止在光滑水平面上,木块左右两侧各有一位持有完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图所示,设子弹均未射穿木块,且两颗子弹与木块之间的作用大小均相同.当两颗子弹均相对于木块静止时,下列判断正确的是( )
质量为m的均匀木块静止在光滑水平面上,木块左右两侧各有一位持有完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图所示,设子弹均未射穿木块,且两颗子弹与木块之间的作用大小均相同.当两颗子弹均相对于木块静止时,下列判断正确的是( )| A. | 木块静止,d1<d2 | B. | 木块静止,d1>d2 | ||
| C. | 木块向右运动,d1<d2 | D. | 木块向左运动,d1=d2 |
分析 对两颗子弹和木块组成的系统而言,合外力为零,总动量守恒,可求出当两颗子弹均相对于木块静止时木块的速度.先以左侧的子弹和木块组成的系统研究,由动量守恒和能量守恒得到d1与子弹速度、质量和木块的关系,再对两颗子弹和木块系统为研究,用同样的方法研究d2,再比较它们的大小.
解答 解:设子弹射入木块前的速度大小为v0,子弹的质量为M,子弹受到的阻力大小为f.当两颗子弹均相对于木块静止时,由动量守恒得
M0v-Mv0=(2M+m)v′,得v′=0,即当两颗子弹均相对于木块静止时,木块的速度为零,即静止.
先对左侧射入木块的子弹和木块组成的系统研究,则有
Mv=(M+m)v1,
由能量守恒得:fd1=$\frac{1}{2}M{v}^{2}$-$\frac{1}{2}(M+m){v}_{1}^{2}$①
再对两颗子弹和木块系统为研究,得
fd2=$\frac{1}{2}(M+m){v}_{1}^{2}$+$\frac{1}{2}M{v}^{2}$ ②
由①②对比得,d1<d2.故A正确.
故选:A
点评 本题运用动量守恒和能量守恒相结合分析子弹与木块相对位移大小的关系,是常用的基本思路.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
16.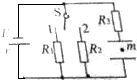 如图所示,电源的电动势为E,内阻未知.当单刀双掷开关掷于1处时,电容器中的质量为m,带电量为+q的带电油滴恰好静止不动,将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,则下列电阻R1:R2正确的是( )
如图所示,电源的电动势为E,内阻未知.当单刀双掷开关掷于1处时,电容器中的质量为m,带电量为+q的带电油滴恰好静止不动,将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,则下列电阻R1:R2正确的是( )
 如图所示,电源的电动势为E,内阻未知.当单刀双掷开关掷于1处时,电容器中的质量为m,带电量为+q的带电油滴恰好静止不动,将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,则下列电阻R1:R2正确的是( )
如图所示,电源的电动势为E,内阻未知.当单刀双掷开关掷于1处时,电容器中的质量为m,带电量为+q的带电油滴恰好静止不动,将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,则下列电阻R1:R2正确的是( )| A. | $\frac{(Eq-ma)dg}{a(Eq-mgd)}$ | B. | $\frac{[qE-m(g-a)d]g}{(g-a)(qE-mgd)}$ | ||
| C. | $\frac{m(g-a)dg}{(Eq-mgd)}$ | D. | $\frac{mgdg}{(g-a)(Eq-mgd)}$ |
14.下列说法正确的是( )
| A. | 库仑通过大量实验分析,得到了真空中两个静止点电荷相互作用规律,并引入电场线形象地描述电荷周围的电场 | |
| B. | 物理学家法拉第通过实验证实了“磁生电”现象的存在,并总结出判断感应电流方向的规律 | |
| C. | 安培首先发现电流磁效应,总结了电流周围磁场方向的判断方法--安培定则 | |
| D. | 美国物理学家密立根利用实验,确定了电荷的不连续性,并测定了元电荷的数值 |
1.如图,某质点做简谐运动的图象.下列说法正确的是( )


| A. | t=0时,质点的速度为零 | |
| B. | t=0.1 s时,质点具有y轴正向最大加速度 | |
| C. | 在0.2 s-0.3 s内质点沿y轴负方向做加速度增大的加速运动 | |
| D. | 在0.5 s-0.6 s内质点沿y轴负方向做加速度减小的加速运动 |
18. 质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )
质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )
 质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )
质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )| A. | 摩擦力做正功,支持力做正功 | B. | 摩擦力做正功,支持力做负功 | ||
| C. | 摩擦力做负功,支持力做正功 | D. | 摩擦力做负功,支持力不做功 |
7. 如图所示,P、Q是两种透明材料制成的两块相同的直角梯形棱镜,叠合在一起组成一个长方体.一束单色光从P的上表面空气中(可看作真空处理)射入,与P上表面的夹角为θ,进入P的折射光刚好垂直通过两棱镜的交界面.已知P、Q所用材料对该单色光的折射率分别为n1、n2,且n1>n2,则下列判断正确的是( )
如图所示,P、Q是两种透明材料制成的两块相同的直角梯形棱镜,叠合在一起组成一个长方体.一束单色光从P的上表面空气中(可看作真空处理)射入,与P上表面的夹角为θ,进入P的折射光刚好垂直通过两棱镜的交界面.已知P、Q所用材料对该单色光的折射率分别为n1、n2,且n1>n2,则下列判断正确的是( )
 如图所示,P、Q是两种透明材料制成的两块相同的直角梯形棱镜,叠合在一起组成一个长方体.一束单色光从P的上表面空气中(可看作真空处理)射入,与P上表面的夹角为θ,进入P的折射光刚好垂直通过两棱镜的交界面.已知P、Q所用材料对该单色光的折射率分别为n1、n2,且n1>n2,则下列判断正确的是( )
如图所示,P、Q是两种透明材料制成的两块相同的直角梯形棱镜,叠合在一起组成一个长方体.一束单色光从P的上表面空气中(可看作真空处理)射入,与P上表面的夹角为θ,进入P的折射光刚好垂直通过两棱镜的交界面.已知P、Q所用材料对该单色光的折射率分别为n1、n2,且n1>n2,则下列判断正确的是( )| A. | 到达Q下表面的光线一定能出射进入空气,且与下表面的夹角大于θ | |
| B. | 到达Q下表面的光线一定能出射进入空气,且与下表面的夹角小于θ | |
| C. | 到达Q下表面的光线不一定能出射进入空气 | |
| D. | 若将P、Q的材料互换,调节从P上表面入射的光线角度,使折射光线依旧垂直通过两棱镜的交界面,则从Q下表面出射的光线与下表面的夹角一定等于θ |
 如图所示,在足够长的光滑水平轨道上有三个小木块A、B、C,质量分别为mA、mB、mC,且mA=mB=1.0kg,mC=2.0kg,其中B与C用一个轻弹簧拴接在一起,开始时整个装置处于静止状态.A和B之间有少许塑胶炸药.现在引爆塑胶炸药,若炸药爆炸产生的能量中有E=9.0J转化为A和B的动能.求:
如图所示,在足够长的光滑水平轨道上有三个小木块A、B、C,质量分别为mA、mB、mC,且mA=mB=1.0kg,mC=2.0kg,其中B与C用一个轻弹簧拴接在一起,开始时整个装置处于静止状态.A和B之间有少许塑胶炸药.现在引爆塑胶炸药,若炸药爆炸产生的能量中有E=9.0J转化为A和B的动能.求: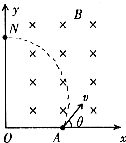 如图所示,有界匀强磁场的磁感应强度为B,区域足够大,方向垂直于纸面向里,直角坐标系xoy的y轴为磁场的左边界,A为固定在x轴上的一个放射源,内装镭核(${\;}_{88}^{226}$Ra)沿着与+x成θ=60°角方向释放一个α粒子后衰变成氡核(Rn),α粒子在y轴上的N点沿-x方向飞离磁场,N点到O点的距离为l,α粒子质量为m,电荷量为q,氡核的质量为M
如图所示,有界匀强磁场的磁感应强度为B,区域足够大,方向垂直于纸面向里,直角坐标系xoy的y轴为磁场的左边界,A为固定在x轴上的一个放射源,内装镭核(${\;}_{88}^{226}$Ra)沿着与+x成θ=60°角方向释放一个α粒子后衰变成氡核(Rn),α粒子在y轴上的N点沿-x方向飞离磁场,N点到O点的距离为l,α粒子质量为m,电荷量为q,氡核的质量为M 如图,手持一根长为L的轻绳的-端在水平桌面上做半径为r、角速度为ω匀速圆周运动,绳始终保持与该圆周相切,绳的另一端系一质量为m的小木块,木块也在桌面上做匀速圆周运动,不计空气阻力,求:
如图,手持一根长为L的轻绳的-端在水平桌面上做半径为r、角速度为ω匀速圆周运动,绳始终保持与该圆周相切,绳的另一端系一质量为m的小木块,木块也在桌面上做匀速圆周运动,不计空气阻力,求: