题目内容
16.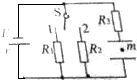 如图所示,电源的电动势为E,内阻未知.当单刀双掷开关掷于1处时,电容器中的质量为m,带电量为+q的带电油滴恰好静止不动,将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,则下列电阻R1:R2正确的是( )
如图所示,电源的电动势为E,内阻未知.当单刀双掷开关掷于1处时,电容器中的质量为m,带电量为+q的带电油滴恰好静止不动,将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,则下列电阻R1:R2正确的是( )| A. | $\frac{(Eq-ma)dg}{a(Eq-mgd)}$ | B. | $\frac{[qE-m(g-a)d]g}{(g-a)(qE-mgd)}$ | ||
| C. | $\frac{m(g-a)dg}{(Eq-mgd)}$ | D. | $\frac{mgdg}{(g-a)(Eq-mgd)}$ |
分析 当单刀双掷开关掷于1处时,带电油滴恰好静止不动,电场力与重力平衡,由此列式得到电容器板间电压,由串联电路分压规律得到板间电压与电阻的关系.将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,根据牛顿第二定律求得板间电压,再由串联电路分压规律得到板间电压与电阻的关系,联立即可求得R1:R2.
解答 解:当单刀双掷开关掷于1处时,带电油滴恰好静止不动,电场力与重力平衡,则有 mg=q$\frac{{U}_{1}}{d}$ ①
根据串联电路电压与电阻成正比的规律得 U1=$\frac{{R}_{1}}{{R}_{1}+r}$E ②
由①②求得 R1=$\frac{mgdr}{qE-mgd}$(r是电源的内阻)
将开关掷于2处时,该油滴以加速度a竖直向下做匀加速运动,根据牛顿第二定律得
mg-q$\frac{{U}_{2}}{d}$=ma ③
由电路的规律得 U2=$\frac{{R}_{2}}{{R}_{2}+r}$E ④
由以上两式解得 R2=$\frac{rd(g-a)}{qE-d(mg-ma)}$
因此可得 $\frac{{R}_{1}}{{R}_{2}}$=$\frac{[qE-m(g-a)d]g}{(g-a)(qE-mgd)}$
故选:B
点评 解决本题的关键要根据电场和电路的知识表示R1和R2的值,要明确电场和电路联系的纽带是电容器的电压,可根据欧姆定律研究电容器的电压.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.下列关于波的干涉和衍射说法正确的是( )
| A. | 在干涉现象中,振动加强点的位移总比减弱点的位移要大 | |
| B. | 光的干涉和衍射都是光波叠加的结果 | |
| C. | 只有当障碍物或孔的尺寸可以跟波长相比,甚至比光的波长还小时,才能产生光的衍射现象 | |
| D. | 用单色光做双缝干涉实验时,将双缝中某一缝挡住,屏上不再出现亮、暗相间的条纹,而是一片亮斑 |
4.以不同的初速度将两个物体A、B同时竖直向上抛出并开始计时,物体A所受空气阻力可忽略,物体B所受空气阻力大小与物体B的速率成正比,下列分别描述两物体运动的v-t图象和a-t图象,可能正确的是( )
| A. |  | B. |  | C. |  | D. |  |
11.一列简谐横波沿x轴负方向传播,a、b为波上的两个质元,某时刻的波形图如图甲所示,从此时刻开始计时,图乙是a、b两个质元中其中一个的振动图象,下列判断正确的是( )

| A. | 波源的振动频率为0.4Hz | |
| B. | 图乙是质元b的振动图象 | |
| C. | 再过0.1s质元a向左运动0.1m | |
| D. | 质元a和质元b在以后的某一时刻振动方向可能相同 |
8. 如图所示,重物G压在纸带上,用一水平力慢速的拉动纸带,重物G会跟着一起运动;若迅速拉动纸带,纸带将会从重物G下面抽出,关于这个现象,下列说法中正确的是( )
如图所示,重物G压在纸带上,用一水平力慢速的拉动纸带,重物G会跟着一起运动;若迅速拉动纸带,纸带将会从重物G下面抽出,关于这个现象,下列说法中正确的是( )
 如图所示,重物G压在纸带上,用一水平力慢速的拉动纸带,重物G会跟着一起运动;若迅速拉动纸带,纸带将会从重物G下面抽出,关于这个现象,下列说法中正确的是( )
如图所示,重物G压在纸带上,用一水平力慢速的拉动纸带,重物G会跟着一起运动;若迅速拉动纸带,纸带将会从重物G下面抽出,关于这个现象,下列说法中正确的是( )| A. | 在慢速拉动纸带时,重物和纸带间的摩擦力大于迅速拉动纸带时重物和纸带间的摩擦力 | |
| B. | 在慢速拉动纸带时,纸带给重物的冲量大 | |
| C. | 在迅速拉动纸带时,纸带给重物的冲量大 | |
| D. | 迅速拉动只带时重物动量的变化大 |
5.在光电效应实验中,两个实验小组分别在各自的实验室,约定用相同频率的单色光,分别照射锌和银的表面,结果都能发生光电效应,如图1,并记录相关数椐.对于这两组实验,下列判断正确的是( )


| A. | 因为材料不同逸出功不同,所以遏止电压Uc不同 | |
| B. | 饱和光电流一定不同 | |
| C. | 光电子的最大初动能不同 | |
| D. | 分别用不同频率的光照射之后绘制Uc-v图象(v为照射光频率,图2为其中一小组绘制的图象),图象的斜率可能不同 |
6. 质量为m的均匀木块静止在光滑水平面上,木块左右两侧各有一位持有完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图所示,设子弹均未射穿木块,且两颗子弹与木块之间的作用大小均相同.当两颗子弹均相对于木块静止时,下列判断正确的是( )
质量为m的均匀木块静止在光滑水平面上,木块左右两侧各有一位持有完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图所示,设子弹均未射穿木块,且两颗子弹与木块之间的作用大小均相同.当两颗子弹均相对于木块静止时,下列判断正确的是( )
 质量为m的均匀木块静止在光滑水平面上,木块左右两侧各有一位持有完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图所示,设子弹均未射穿木块,且两颗子弹与木块之间的作用大小均相同.当两颗子弹均相对于木块静止时,下列判断正确的是( )
质量为m的均匀木块静止在光滑水平面上,木块左右两侧各有一位持有完全相同步枪和子弹的射击手.首先左侧射手开枪,子弹水平射入木块的最大深度为d1,然后右侧射手开枪,子弹水平射入木块的最大深度为d2,如图所示,设子弹均未射穿木块,且两颗子弹与木块之间的作用大小均相同.当两颗子弹均相对于木块静止时,下列判断正确的是( )| A. | 木块静止,d1<d2 | B. | 木块静止,d1>d2 | ||
| C. | 木块向右运动,d1<d2 | D. | 木块向左运动,d1=d2 |

 如图所示,磁感应强度大小B=0.3T、方向垂直纸面向里的匀强磁场分布在半径R=0.20m的圆形区域内,圆的水平直径上方竖直分界线MN的左侧有水平向右的匀强电场,竖直分界线PQ右侧有水平向左的匀强电场,电场强度大小均为E=4$\sqrt{3}$×104V/m,在圆的水平直径AOC的A点有一粒子源,同时沿直径AO方向射出速度分别为v1=$\sqrt{3}$×106m/s和v2=3$\sqrt{3}$×106m/s的带正电的两个粒子,如果粒子的比荷$\frac{q}{m}$=5.0×107C/kg,且不计粒子重力及粒子间的相互作用.求:
如图所示,磁感应强度大小B=0.3T、方向垂直纸面向里的匀强磁场分布在半径R=0.20m的圆形区域内,圆的水平直径上方竖直分界线MN的左侧有水平向右的匀强电场,竖直分界线PQ右侧有水平向左的匀强电场,电场强度大小均为E=4$\sqrt{3}$×104V/m,在圆的水平直径AOC的A点有一粒子源,同时沿直径AO方向射出速度分别为v1=$\sqrt{3}$×106m/s和v2=3$\sqrt{3}$×106m/s的带正电的两个粒子,如果粒子的比荷$\frac{q}{m}$=5.0×107C/kg,且不计粒子重力及粒子间的相互作用.求: