��Ŀ����
11��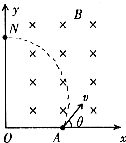 ��ͼ��ʾ���н���ǿ�ų��ĴŸ�Ӧǿ��ΪB�������㹻����ֱ��ֽ�����ֱ������ϵxoy��y��Ϊ�ų�����߽磬AΪ�̶���x���ϵ�һ������Դ����װ�غˣ�${\;}_{88}^{226}$Ra��������+x�ɦ�=60��Ƿ����ͷ�һ�������Ӻ�˥���뱺ˣ�Rn������������y���ϵ�N����-x�������ų���N�㵽O��ľ���Ϊl������������Ϊm�������Ϊq��뱺˵�����ΪM
��ͼ��ʾ���н���ǿ�ų��ĴŸ�Ӧǿ��ΪB�������㹻����ֱ��ֽ�����ֱ������ϵxoy��y��Ϊ�ų�����߽磬AΪ�̶���x���ϵ�һ������Դ����װ�غˣ�${\;}_{88}^{226}$Ra��������+x�ɦ�=60��Ƿ����ͷ�һ�������Ӻ�˥���뱺ˣ�Rn������������y���ϵ�N����-x�������ų���N�㵽O��ľ���Ϊl������������Ϊm�������Ϊq��뱺˵�����ΪM��1��д���غ˵�˥�䷽��
��2������غ�˥��ʱ�ͷŵ�����ȫ����Ϊ�����Ӻ�뱺˵Ķ��ܣ���һ��ԭ����ֹ���غ�˥��ʱ�ų���������
���� ��1���������ͺ˵�����غ�д�˷�Ӧ���̣�
��2���غ�˥��ų������Ӻ�뱺ˣ��ֱ��ڴų���������Բ���˶������ݽ�Ϲ�ϵ����������ڴų���������Բ���˶��İ뾶�����ݰ뾶��ʽ����ٶȣ���������ӵĶ��ܣ�˥������ж����غ㣬���뱺˷���Ķ��ܣ����߶���֮�ͼ�Ϊԭ����ֹ���غ�˥��ʱ�ų���������
��� �⣺��1���غ�˥�䷽��Ϊ��${\;}_{88}^{226}$Ra��${\;}_{86}^{222}$Ra+${\;}_{2}^{4}$He
��2��˥���ͷŵ���������E=EKM+EKm
˥����̸��ݶ����غ㣺0=Pm-PM
������$\frac{{{E_{KM}}}}{{{E_{Km}}}}=\frac{m}{M}$
�ɼ��ι�ϵ��R+Rcos��=l
�������ڴų���������Բ���˶���$qvB=m\frac{v^2}{R}$
�����ϼ�ʽ��ã�$��E=\frac{M+m}{M}•\frac{{2{{��qBl��}^2}}}{9m}$
�𣺣�1���غ˵�˥�䷽��${\;}_{88}^{226}$Ra��${\;}_{86}^{222}$Ra+${\;}_{2}^{4}$He��
��2��һ��ԭ����ֹ���غ�˥��ʱ�ų�������$\frac{M+m}{M}•\frac{2��qBl��^{2}}{9m}$��
���� ���⿼���˺˷�Ӧ���̣��Ͷ����غ㶨�ɣ��ؼ���֪��˭��˭�����غ㼰��������ǿ�ų��е��˶������

 �ڹ⻬�����Ϸ�һ��С����С������˷���һֻ���ӣ���ˮƽ���������£������Ӵ���������Ҷˣ����һ��С�����ƶ�����һ��С��δ���ƶ���������������У�������
�ڹ⻬�����Ϸ�һ��С����С������˷���һֻ���ӣ���ˮƽ���������£������Ӵ���������Ҷˣ����һ��С�����ƶ�����һ��С��δ���ƶ���������������У�������| A�� | �����복��֮��Ħ����һ���� | B�� | F�����Ĺ�һ���� | ||
| C�� | ���ӻ�õļ��ٶȲ�һ���� | D�� | ���ӻ�õĶ���һ���� |
 ����Ϊm�ľ���ľ�龲ֹ�ڹ⻬ˮƽ���ϣ�ľ�������������һλ������ȫ��ͬ��ǹ���ӵ�������֣�����������ֿ�ǹ���ӵ�ˮƽ����ľ���������Ϊd1��Ȼ���Ҳ����ֿ�ǹ���ӵ�ˮƽ����ľ���������Ϊd2����ͼ��ʾ�����ӵ���δ�䴩ľ�飬�������ӵ���ľ��֮������ô�С����ͬ���������ӵ��������ľ�龲ֹʱ�������ж���ȷ���ǣ�������
����Ϊm�ľ���ľ�龲ֹ�ڹ⻬ˮƽ���ϣ�ľ�������������һλ������ȫ��ͬ��ǹ���ӵ�������֣�����������ֿ�ǹ���ӵ�ˮƽ����ľ���������Ϊd1��Ȼ���Ҳ����ֿ�ǹ���ӵ�ˮƽ����ľ���������Ϊd2����ͼ��ʾ�����ӵ���δ�䴩ľ�飬�������ӵ���ľ��֮������ô�С����ͬ���������ӵ��������ľ�龲ֹʱ�������ж���ȷ���ǣ�������| A�� | ľ�龲ֹ��d1��d2 | B�� | ľ�龲ֹ��d1��d2 | ||
| C�� | ľ�������˶���d1��d2 | D�� | ľ�������˶���d1=d2 |

| A�� | 2��3 | B�� | 4��9 | C�� | 1��2 | D�� | 1��1 |
 ��ͼ��ʾ����һ�뾶ΪR�İ�Բ����������ڴ�ֱ��Բ���������ǿ�ų���ͼ��δ���������Ÿ�Ӧǿ�ȵĴ�СΪB����Բ��O����һ����Դ�������ش�ֱ�ڴų��IJ�ͬ������ų�����������Ϊm�������Ϊq���ٶȴ�С��Ϊ$\frac{qBR}{m}$�Ĵ���������ӣ������������ƣ�������˵����ȷ���ǣ�������
��ͼ��ʾ����һ�뾶ΪR�İ�Բ����������ڴ�ֱ��Բ���������ǿ�ų���ͼ��δ���������Ÿ�Ӧǿ�ȵĴ�СΪB����Բ��O����һ����Դ�������ش�ֱ�ڴų��IJ�ͬ������ų�����������Ϊm�������Ϊq���ٶȴ�С��Ϊ$\frac{qBR}{m}$�Ĵ���������ӣ������������ƣ�������˵����ȷ���ǣ�������| A�� | �ڰ�Բ���ϸ�������������� | |
| B�� | �����ڴų����˶����ʱ��Ϊ$\frac{��m}{3qB}$ | |
| C�� | �ų������Ӳ��ܴﵽ���������Ϊ$\frac{1}{12}$��R2 | |
| D�� | �Ӱ�Բ��������������ڴų����˶���ʱ����ͬ |
| A�� | $\frac{1}{pq}$�� | B�� | $\frac{q}{p}$�� | C�� | $\frac{p}{q}$�� | D�� | pq�� |
 ��ͼ��ʾ���Ÿ�Ӧǿ�ȴ�СB=0.3T������ֱֽ���������ǿ�ų��ֲ��ڰ뾶R=0.20m��Բ�������ڣ�Բ��ˮƽֱ���Ϸ���ֱ�ֽ���MN�������ˮƽ���ҵ���ǿ�糡����ֱ�ֽ���PQ�Ҳ���ˮƽ�������ǿ�糡���糡ǿ�ȴ�С��ΪE=4$\sqrt{3}$��104V/m����Բ��ˮƽֱ��AOC��A����һ����Դ��ͬʱ��ֱ��AO��������ٶȷֱ�Ϊv1=$\sqrt{3}$��106m/s��v2=3$\sqrt{3}$��106m/s�Ĵ�������������ӣ�������ӵıȺ�$\frac{q}{m}$=5.0��107C/kg���Ҳ����������������Ӽ������ã���
��ͼ��ʾ���Ÿ�Ӧǿ�ȴ�СB=0.3T������ֱֽ���������ǿ�ų��ֲ��ڰ뾶R=0.20m��Բ�������ڣ�Բ��ˮƽֱ���Ϸ���ֱ�ֽ���MN�������ˮƽ���ҵ���ǿ�糡����ֱ�ֽ���PQ�Ҳ���ˮƽ�������ǿ�糡���糡ǿ�ȴ�С��ΪE=4$\sqrt{3}$��104V/m����Բ��ˮƽֱ��AOC��A����һ����Դ��ͬʱ��ֱ��AO��������ٶȷֱ�Ϊv1=$\sqrt{3}$��106m/s��v2=3$\sqrt{3}$��106m/s�Ĵ�������������ӣ�������ӵıȺ�$\frac{q}{m}$=5.0��107C/kg���Ҳ����������������Ӽ������ã��� ijͬѧ������ʵ���ҵ�ʱ����һ�����εIJ����أ����������ʶ��������ֻ�ܿ��������ԼΪ10����Ϊ�˲�ò����ص����裬ʵ�������ṩ�������ģ�
ijͬѧ������ʵ���ҵ�ʱ����һ�����εIJ����أ����������ʶ��������ֻ�ܿ��������ԼΪ10����Ϊ�˲�ò����ص����裬ʵ�������ṩ�������ģ�