题目内容
14.如图甲所示空间存在一个匀强磁场,磁场方向垂直纸面向里.梯形线圈abcd由图示位罝开始以速度v匀速进入磁场.计时开始时bc边与磁场区域边界重合,则在线圈进入磁场区域的整个过程中,图乙可能表示的是( )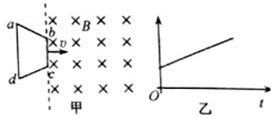
| A. | 线圈所受安培力F随时间t变化的关系 | |
| B. | 感应电动势E随时间t变化的关系 | |
| C. | 流过线圈回路的电量q随时间t变化的关系 | |
| D. | 通过线圈磁通量变化率$\frac{△φ}{△t}$随时间t变化的关系 |
分析 一个梯形线圈切割磁感线,由于切割的有效长度均匀增加,因此感感应电动势也均匀增大,而电阻不变,所以感应电流也均匀增大.据安培力的公式F=BIL知,电流I与时间t均随时间增大,所以安培力是时间的二次函数;至于电量q=It,也是时间的二次函数;感应电动势与磁通量的变化率成正比,所以E与$\frac{△∅}{△t}$是同样变化的.
解答 解:梯形线圈以恒定的速度v进入磁场,其有效切割长度L=L0+kvt,其中L0为bc边的长、k为与两个顶角有关的常数,所以产生的感应电动势E=BLv=B(L0+kvt)v.
A、感应电流正比于感应电动势,安培力F=BIL,正比于电流、正比于L.由此可知安培力是时间t的二次函数,所以选项A错误.
B、由上述分析,E=BLv=B(L0+kvt)v,感应电动势是时间t的一次函数,所以选项B正确.
C、通过线圈的电量$q=\overline{I}△t=\frac{\overline{E}}{R}△t=\frac{△∅}{R}=\frac{\frac{{L}_{0}+{L}_{0}+kvt}{2}×vt}{R}$,显然是时间t的二次函数,所以选项C错误.
D、根据法拉第电磁感应定律感应电动势与磁通量的变化率成正比,B正确,所以选项D正确.
故选:BD
点评 本题的关键点在于切割时,切割的有效长度发生变化,从而导致感应电动势变化,感应电流变化,必须从基本公式出发,确定每一个物理量是时间的几次函数,才能判断正误.

练习册系列答案
相关题目
19.一物体做直线运动的速度-时间图象如图所示,则下列说法中正确的是( )


| A. | 第 1 s 内的加速度大于第 5 s 内的加速度 | |
| B. | 第 1 s 内与第 5 s 内的加速度方向相同 | |
| C. | 第Ⅰ段与第Ⅲ段平均速度相等 | |
| D. | 第Ⅰ段和第Ⅲ段的加速度与速度的方向都相同 |
20.下列全为矢量的一组是( )
| A. | 位移 速度 加速度 | B. | 位移 时间 加速度 | ||
| C. | 路程 体重 温度 | D. | 身高 速率 速度 |

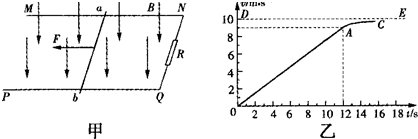 如图甲所示,空间存在B=0.5T,方向竖直向下的匀强磁场,MN、PQ是相互平行的粗糙的长直导轨,处于同一水平面内,其间距L=0.2m,R是连在导轨一端的电阻,ab是跨接在导轨上质量m=0.1kg的导体棒,从零时刻开始,通过一小型电动机对ab棒施加一个牵引力F,方向水平向左,使其从静止开始沿导轨做直线运动,此过程中棒始终保持与导轨垂直且接触良好,图乙是棒的速度-时间图象,其中OA段是直线,AC段是曲线,DE是曲线图象的渐近线,小型电动机在12s末达到额定功率P=4.5W,此后功率保持不变,除R以外,其余部分的电阻均不计,g=10m/s2
如图甲所示,空间存在B=0.5T,方向竖直向下的匀强磁场,MN、PQ是相互平行的粗糙的长直导轨,处于同一水平面内,其间距L=0.2m,R是连在导轨一端的电阻,ab是跨接在导轨上质量m=0.1kg的导体棒,从零时刻开始,通过一小型电动机对ab棒施加一个牵引力F,方向水平向左,使其从静止开始沿导轨做直线运动,此过程中棒始终保持与导轨垂直且接触良好,图乙是棒的速度-时间图象,其中OA段是直线,AC段是曲线,DE是曲线图象的渐近线,小型电动机在12s末达到额定功率P=4.5W,此后功率保持不变,除R以外,其余部分的电阻均不计,g=10m/s2 如图所示,两条足够长的平行金属导轨固定在水平面上,导轨平面与水平面间的夹角为θ=37°,导轨间距为L=1m,与导轨垂直的两条边界线MN、PQ内有垂直于导轨平面向上的匀强磁场,磁感应强度大小为B0=1T,MN与PQ间的距离为d=2m,两个完全相同的金属棒ab、ef用长为d=2m的绝缘轻杆固定成“工”字型装置,开始时金属棒ab与MN重合,已知每根金属棒的质量为m=0.05kg,电阻为R=5Ω,导轨电阻不计,金属棒与导轨间的动摩擦因数μ=0.5,在t=0时,将“工”字型装置由静止释放,当ab边滑行至PQ处恰好开始做匀速运动,已知sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,求:
如图所示,两条足够长的平行金属导轨固定在水平面上,导轨平面与水平面间的夹角为θ=37°,导轨间距为L=1m,与导轨垂直的两条边界线MN、PQ内有垂直于导轨平面向上的匀强磁场,磁感应强度大小为B0=1T,MN与PQ间的距离为d=2m,两个完全相同的金属棒ab、ef用长为d=2m的绝缘轻杆固定成“工”字型装置,开始时金属棒ab与MN重合,已知每根金属棒的质量为m=0.05kg,电阻为R=5Ω,导轨电阻不计,金属棒与导轨间的动摩擦因数μ=0.5,在t=0时,将“工”字型装置由静止释放,当ab边滑行至PQ处恰好开始做匀速运动,已知sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,求: 竖直放置的两根表面光滑的平行金属导轨,间距为d,导轨上端连接一阻值为R的定值电阻.两导轨间存在着与导轨平面垂直且方向相反的匀强磁场区域Ⅰ和Ⅱ,磁感应强度大小均为B.当质量为m0的金属棒ab从图中位置由静止释放后,刚进入区域Ⅰ即做匀速运动;若在金属棒的中点挂上质量为△m的小沙桶,仍从图示位置由静止释放金属棒ab,棒匝磁场中某一位置可达到最大速度;若逐渐增大小沙桶的质量,棒所达到的最大速度vm随之改变.已知重力加速度大小为g,区域Ⅱ足够大,不计导轨和金属棒ab的电阻,金属棒一直与导轨垂直且接触良好.
竖直放置的两根表面光滑的平行金属导轨,间距为d,导轨上端连接一阻值为R的定值电阻.两导轨间存在着与导轨平面垂直且方向相反的匀强磁场区域Ⅰ和Ⅱ,磁感应强度大小均为B.当质量为m0的金属棒ab从图中位置由静止释放后,刚进入区域Ⅰ即做匀速运动;若在金属棒的中点挂上质量为△m的小沙桶,仍从图示位置由静止释放金属棒ab,棒匝磁场中某一位置可达到最大速度;若逐渐增大小沙桶的质量,棒所达到的最大速度vm随之改变.已知重力加速度大小为g,区域Ⅱ足够大,不计导轨和金属棒ab的电阻,金属棒一直与导轨垂直且接触良好. 如图所示,倾角θ=30°的斜面足够长,OA段光滑,A点下方粗糙且与物体C间的摩擦因数μ1=$\frac{1}{4\sqrt{3}}$.水平面上足够长OB段粗糙且μ2=0.5,B点右侧水平面光滑.OB之间有与水平方向β角(sinβ=$\frac{\sqrt{10}}{10}$,cosβ=$\frac{3\sqrt{10}}{10}$),斜向右上方、大小E=$\sqrt{10}$×105V/m的匀强电场.C、D均可视为质点,质量分别为mC=4kg,mD=1kg,C不带电,D带电q=+1×10-4C,用轻质细线将C、D连在一起,跨过光滑的定滑轮,分别将C、D置于斜面及水平面上的P和Q点,用手按住D,系统保持由静止.松手后C、D均由静止开始运动,B、Q间距离d=1m,A、P间距离为2d,细绳与滑轮之间的摩擦不计.细线始终处于拉紧状态.(g=10m/s2),求:
如图所示,倾角θ=30°的斜面足够长,OA段光滑,A点下方粗糙且与物体C间的摩擦因数μ1=$\frac{1}{4\sqrt{3}}$.水平面上足够长OB段粗糙且μ2=0.5,B点右侧水平面光滑.OB之间有与水平方向β角(sinβ=$\frac{\sqrt{10}}{10}$,cosβ=$\frac{3\sqrt{10}}{10}$),斜向右上方、大小E=$\sqrt{10}$×105V/m的匀强电场.C、D均可视为质点,质量分别为mC=4kg,mD=1kg,C不带电,D带电q=+1×10-4C,用轻质细线将C、D连在一起,跨过光滑的定滑轮,分别将C、D置于斜面及水平面上的P和Q点,用手按住D,系统保持由静止.松手后C、D均由静止开始运动,B、Q间距离d=1m,A、P间距离为2d,细绳与滑轮之间的摩擦不计.细线始终处于拉紧状态.(g=10m/s2),求: 一长为L的细线,上端固定于O点,下端拴一质量为m、带电荷量为q的小球,处于如图所示的水平向右的匀强电场中.开始时,将细线拉成水平,释放后小球从A点由静止沿圆弧开始向下摆动,当细线转过60°角时,小球到达B点速度恰好为零.试求:
一长为L的细线,上端固定于O点,下端拴一质量为m、带电荷量为q的小球,处于如图所示的水平向右的匀强电场中.开始时,将细线拉成水平,释放后小球从A点由静止沿圆弧开始向下摆动,当细线转过60°角时,小球到达B点速度恰好为零.试求: