题目内容
2.如图甲所示是某同学设计的一种振动发电装置的示意图,它的结构是一个套在辐向形永久磁铁槽中的半径为r=0.10m、匝数n=100的线圈,磁场的磁感线均沿半径方向均匀分布(其右视图如图乙所示).在线圈所在位置磁感应强度B的大小均为B=$\frac{\sqrt{2}}{π}$T,线圈的电阻为R1=0.50Ω,它的引出线接有R2=9.5Ω的小电珠L.外力推动线圈框架的P端,使线圈沿轴线做往复运动,便有电流通过电珠.当线圈运动速度v随时间t变化的规律如图丙所示时(摩擦等损耗不计),从t=0时刻开始计时.求:
(1)写出线圈中产生的感应电动势的瞬时值表达式以及电压表中的示数;
(2)通电40s小电珠L消耗的电能;
(3)t=0.1s时外力F的大小.
分析 (1)当线圈运动速度v最大时,线圈产生的感应电动势最大,感应电流达到最大.线圈做切割磁感线产生的感应电动势E=2nπrBv,求出感应电动势的最大值,再由欧姆定律求解小电珠中电流的最大值.线圈中产生的是正弦式电流,电压表测量灯泡电压的有效值.由电流最大值求出电压的最大值,再求解有效值,从而求得电压表的示数.
(2)根据焦耳定律求解产生的热量;
(3)线圈做简谐运动,t=0.1s时线圈通过平衡位置,外力等于安培力.
解答 解:(1)电动势最大值${E}_{m}=nBL{v}_{m}=nB•2πr•{v}_{m}=40\sqrt{2}V$
线圈转动的角速度$ω=\frac{2π}{T}=5π\\;rad/s$
电动势的瞬时值$e=40\sqrt{2}sin5πt\\;(V)$
电动势的有效值$E=\frac{{E}_{m}}{\sqrt{2}}=\frac{40\sqrt{2}}{\sqrt{2}}V=40V$
电流的有效值$I=\frac{E}{{R}_{1}+{R}_{2}}=\frac{40}{0.5+9.5}A=4A$
电压表的示数U=IR2=4×9.5V=38V
(2)根据焦耳定律可得:$Q={I}^{2}{R}_{2}t={4}^{2}×9.5×40J=6080J$
(3)t=0.1s时$e={E}_{m}=40\sqrt{2}V$
电流强度i=Im=$\frac{{E}_{m}}{{R}_{1}+{R}_{2}}=\frac{40\sqrt{2}}{10}A=4\sqrt{2}A$
此时线圈的速度最大而加速度为零,
则:F=FA=nBIm•2πr=100×$\frac{\sqrt{2}}{π}$×$4\sqrt{2}$×2×π×0.1N=160N.
答:(1)线圈中产生的感应电动势的瞬时值表达式为$e=40\sqrt{2}sin5πt\\;(V)$,电压表中的示数为38V;
(2)通电40s小电珠L消耗的电能为6080J;
(3)t=0.1s时外力F的大小为160N.
点评 本题考查导线切割磁感线产生感应电动势公式及正弦式电流有效值与最大值之间的关系,关键是电动势的大小表达式.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
| A. | t=0时,A比B的速度快 | |
| B. | B在t2时刻追上A,并在此后跑在A的前面 | |
| C. | B开始时速度比A小,t1时刻后速度比A大 | |
| D. | t1到t2之间A静止不动 |
| A. | 甲质点的速度大于乙质点的速度 | |
| B. | 乙质点的速度大于甲质点的速度 | |
| C. | 因二者的方向不同,故无法比较其速度的大小 | |
| D. | 这里的正负号与数学中的正负号意义完全相同 |
 如图所示,匀强电场场强为1×103N/C,ab=dc=4cm,bc=ad=3cm,则下述计算结果正确的是( )
如图所示,匀强电场场强为1×103N/C,ab=dc=4cm,bc=ad=3cm,则下述计算结果正确的是( )| A. | ab之间的电势差为4000V | |
| B. | ac之间的电势差为50V | |
| C. | 将q=-5×10-3C的点电荷沿矩形路径abcda移动一周,静电力做功为零 | |
| D. | 将q=-5×10-3C的点电荷沿abc或adc从a移动到c静电力做功都是-0.25J |
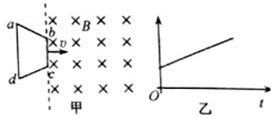
| A. | 线圈所受安培力F随时间t变化的关系 | |
| B. | 感应电动势E随时间t变化的关系 | |
| C. | 流过线圈回路的电量q随时间t变化的关系 | |
| D. | 通过线圈磁通量变化率$\frac{△φ}{△t}$随时间t变化的关系 |
 如图所示,用绝缘细线栓一个带负电的小球,带电量大小为q,让它在竖直向下的匀强电场中(场强为E)绕O点做竖直平面内的匀速圆周运动,a、b两点分别是最高点和最低点,不计空气阻力,则下列说法中正确的是( )
如图所示,用绝缘细线栓一个带负电的小球,带电量大小为q,让它在竖直向下的匀强电场中(场强为E)绕O点做竖直平面内的匀速圆周运动,a、b两点分别是最高点和最低点,不计空气阻力,则下列说法中正确的是( )| A. | 小球在运动中机械能守恒 | B. | 小球经过a点时,机械能最大 | ||
| C. | 小球质量为$\frac{Eq}{g}$ | D. | 小球经过a点时,电势能最大 |
 研究表明,一般人的刹车反应时间(即图甲中“反应过程”所用时间)t0=0.4s,但饮酒会导致反应时间延长,在某次实验中,志愿者少量饮酒后驾车以v0=72km/h的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39m.汽车刹车减速过程中汽车速度v与位移s的关系曲线如图乙所示,此过程可视为匀变速直线运动,取重力加速度大小g=10m/s2,求:
研究表明,一般人的刹车反应时间(即图甲中“反应过程”所用时间)t0=0.4s,但饮酒会导致反应时间延长,在某次实验中,志愿者少量饮酒后驾车以v0=72km/h的速度在试验场的水平路面上匀速行驶,从发现情况到汽车停止,行驶距离L=39m.汽车刹车减速过程中汽车速度v与位移s的关系曲线如图乙所示,此过程可视为匀变速直线运动,取重力加速度大小g=10m/s2,求:
 如图所示,把长L=0.5m的导体棒,垂直放入磁感应强度B=1T的匀强磁场中.当导体棒中通有方向水平向右、大小I=2A的电流时,导体棒受到的安培力大小F=1N,方向向上(填“向上”或“向下).
如图所示,把长L=0.5m的导体棒,垂直放入磁感应强度B=1T的匀强磁场中.当导体棒中通有方向水平向右、大小I=2A的电流时,导体棒受到的安培力大小F=1N,方向向上(填“向上”或“向下).