题目内容
18.质量为m,长为L的木板B静止在光滑水平面上,其右端放质量为$\frac{1}{3}$m的物块C,物块C可看做质点,质量为m的木板A以速度v0在水平面上向右运动,与B发生弹性正碰,碰撞时间极短,整个运动过程中物块C始终没有滑离木板B,B和C之间的动摩擦因数为μ,求物块C相对于B静止时距B右端的距离.
分析 对A、B组成的系统运用动量守恒和能量守恒求出B碰后的速度,对BC组成的系统运用动量守恒求出共同的速度,结合能量守恒求出相对滑动的距离.
解答 解:由题意可知,木板A和B发生弹性正碰,碰后A的速度v1,B的速度为v2,对A、B组成的系统,由动量守恒和能量守恒定律得
mv0=mv1+mv2,
$\frac{1}{2}m{{v}_{0}}^{2}=\frac{1}{2}m{{v}_{1}}^{2}+\frac{1}{2}m{{v}_{2}}^{2}$
解得 v1=0,v2=v0
A与B弹开后,B、C组成的系统动量守恒,B、C最后的共同速度为v3
$m{v}_{2}=(m+\frac{1}{3}m){v}_{3}$
对木板B和物块C,由系统能量守恒得
${F}_{f}{s}_{相}=\frac{1}{2}m{{v}_{2}}^{2}-\frac{1}{2}m{{v}_{3}}^{2}-$$\frac{1}{2}(\frac{1}{3}m){{v}_{3}}^{2}$,
${F}_{f}=μ\frac{1}{3}mg$
解得 ${s}_{相}=\frac{3{{v}_{0}}^{2}}{8μg}$.
答:物块C相对于B静止时距B右端的距离为$\frac{3{{v}_{0}}^{2}}{8μg}$.
点评 本题考查了动量守恒和能量守恒的综合运用,综合性较强,对学生的能力要求较高,需加强这方面的训练.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
8. 如图所示,有三个斜面a、b、c,底边的长分别为L、L、3L,高度分别为3h、h、h.某物体与三个斜面间的动摩擦因数都相同,这个物体分别沿三个斜面从顶端由静止下滑到底端.三种情况相比较,下列说法正确的是( )
如图所示,有三个斜面a、b、c,底边的长分别为L、L、3L,高度分别为3h、h、h.某物体与三个斜面间的动摩擦因数都相同,这个物体分别沿三个斜面从顶端由静止下滑到底端.三种情况相比较,下列说法正确的是( )
 如图所示,有三个斜面a、b、c,底边的长分别为L、L、3L,高度分别为3h、h、h.某物体与三个斜面间的动摩擦因数都相同,这个物体分别沿三个斜面从顶端由静止下滑到底端.三种情况相比较,下列说法正确的是( )
如图所示,有三个斜面a、b、c,底边的长分别为L、L、3L,高度分别为3h、h、h.某物体与三个斜面间的动摩擦因数都相同,这个物体分别沿三个斜面从顶端由静止下滑到底端.三种情况相比较,下列说法正确的是( )| A. | 物体损失的机械能2△Ec=2△Eb=4△Ea | |
| B. | 因摩擦产生的热量3Qa=3Qb=Qc | |
| C. | 物体到达底端的动能Eka=3Ekb=3Ekc | |
| D. | 因摩擦产生的热量4Qa=2Qb=Qc |
13.某人将质量为1kg的物体沿竖直方向由静止向上提起1m时,物体的速度大小为2m/s,此过程中人对物体做功为(重力加速度取10m/s2)( )
| A. | 2J | B. | 10J | C. | 12J | D. | 20J |
7.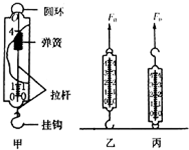 实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )
实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )
 实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )
实验室常用的弹簧测力计如图甲所示,有挂钩的拉杆与弹簧相连,并固定在外壳一端O上,外壳上固定一个圆环,可以认为弹簧测力计的总质量主要集中在外壳(重量为G)上,弹簧和拉杆的质量忽略不计.再将该弹簧测力计以两种方式固定于地面上,如图乙、丙所示,分别用恒力F0竖直向上拉弹簧测力计,静止时弹簧测力计的读数为( )| A. | 乙图读数F0-G,丙图读数F0+G | B. | 乙图读数F0+G,丙图读数F0-G | ||
| C. | 乙图读数F0,丙图读数F0-G | D. | 乙图读数F0-G,丙图读数F0 |
 U型池单板滑雪是深受滑雪者喜爱的项目,其场地(横截面)如图所示,AB,CD均为半径R=3.6m的$\frac{1}{4}$圆轨道,BC为水平轨道,一质量m=60kg的运动员从A点以某一速度滑下,经U型轨道从D点竖直向上飞出,在D点上方完成动作的时间t=1.2s.然后又从D点滑入U型池,若不计阻力和摩擦,运动员可看成质点,求运动员在U型池滑行过程中,U型池对运动员的最大弹力.
U型池单板滑雪是深受滑雪者喜爱的项目,其场地(横截面)如图所示,AB,CD均为半径R=3.6m的$\frac{1}{4}$圆轨道,BC为水平轨道,一质量m=60kg的运动员从A点以某一速度滑下,经U型轨道从D点竖直向上飞出,在D点上方完成动作的时间t=1.2s.然后又从D点滑入U型池,若不计阻力和摩擦,运动员可看成质点,求运动员在U型池滑行过程中,U型池对运动员的最大弹力. 如图所示,在真空中相距为L=0.2m的足够长金属导轨MN和PQ与水平方向成α=37°倾斜放置,长度也均为L的质量为m1=0.1kg的金属棒ab 和质量为m2=0.2kg的金属棒cd,通过固定在金属棒两端的金属轻滑环套在套在导轨上,虚线OO′上方的匀强磁场的方向垂直于斜面向上,虚线OO′下方的匀强磁场的方向平行于斜面向上,两处的匀强磁场的磁感应强度大小均为B=1T.ab两端的滑环是光滑的,cd两端的滑环与导轨间的动摩擦因数为0.25,两金属棒在导轨间的电阻均为R0=0.5Ω,导轨和滑环的电阻不计,现金属棒ab在沿斜面向上的外力F的作用下,从静止开始沿导轨向上做加速度为a=2m/s2的匀加速直线运动,在金属棒ab刚开始运动的同时,金属棒cd也由静止释放.sin37°=0.6,cos37°=0.8,重力加速度为g=10m/s2.求:
如图所示,在真空中相距为L=0.2m的足够长金属导轨MN和PQ与水平方向成α=37°倾斜放置,长度也均为L的质量为m1=0.1kg的金属棒ab 和质量为m2=0.2kg的金属棒cd,通过固定在金属棒两端的金属轻滑环套在套在导轨上,虚线OO′上方的匀强磁场的方向垂直于斜面向上,虚线OO′下方的匀强磁场的方向平行于斜面向上,两处的匀强磁场的磁感应强度大小均为B=1T.ab两端的滑环是光滑的,cd两端的滑环与导轨间的动摩擦因数为0.25,两金属棒在导轨间的电阻均为R0=0.5Ω,导轨和滑环的电阻不计,现金属棒ab在沿斜面向上的外力F的作用下,从静止开始沿导轨向上做加速度为a=2m/s2的匀加速直线运动,在金属棒ab刚开始运动的同时,金属棒cd也由静止释放.sin37°=0.6,cos37°=0.8,重力加速度为g=10m/s2.求: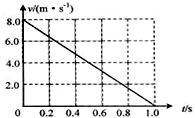 一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机作出了小物块上滑过程的v-t图线,如图所示.(取sin 37°=0.6,cos 37°=0.8,g=10m/s2)求:
一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机作出了小物块上滑过程的v-t图线,如图所示.(取sin 37°=0.6,cos 37°=0.8,g=10m/s2)求: