题目内容
10.两个小球A和B在光滑的水平面上沿同一直线运动,A的质量为1kg,速度大小为6m/s,B的质量为2kg,速度大小为3m/s,求下列各种情况下碰撞后的速度:(1)A和B都向右运动,碰撞后结合在一起,v共=4m/s;
(2)A向右运动,B向左运动,碰撞后结合在一起,v共=0m/s;
(3)A和B都向右运动,碰撞后A仍向右运动,速度大小为2m/s,碰撞后B的速度vB′=5m/s;
(4)A向右运动,B向左运动,碰撞后A向左运动,速度大小为4m/s,碰撞后B的速度vB′=2m/s.
分析 对A、B两球组成的系统研究,运用动量守恒定律求出速度的大小.
解答 解:(1)A、B组成的系统动量守恒,规定向右为正方向,根据动量守恒定律得,
m1v1+m2v2=(m1+m2)v共,
解得${v}_{共}=\frac{1×6+2×3}{3}m/s=4m/s$.
(2)规定向右为正方向,根据动量守恒得,m1v1+m2v2=(m1+m2)v共,
${v}_{共}=\frac{1×6-2×3}{3}m/s=0m/s$.
(3)规定向右为正方向,根据动量守恒得,m1v1+m2v2=m1v1′+m2vB,
解得${v}_{B}=\frac{1×6+2×3-1×2}{2}m/s=5m/s$.
(3)规定向右为正方向,根据动量守恒得,m1v1+m2v2=m1vA+m2vB,
代入数据得,1×6-2×3=1×(-4)+2vB,解得vB=2m/s.
故答案为:(1)4m/s,(2)0m/s,(3)5m/s,(4)2m/s.
点评 本题考查了动量守恒定律的基本运用,知道A、B碰撞前后动量守恒,注意公式的矢量性.

练习册系列答案
相关题目
1.太空垃圾如人造卫星一样按一定的轨道绕地球飞行,若某大块太空垃圾在稀薄空气阻力的作用下,轨道半径逐渐变小.这个过程中,太空垃圾的( )
| A. | 动能逐渐减小 | B. | 向心加速度逐渐减小 | ||
| C. | 机械能逐渐减小 | D. | 运动周期逐渐减小 |
19.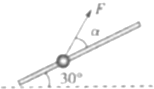 如图所示,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力F作用下,小球沿杆由底端匀速运动到顶端.已知小球与斜杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,则关于拉力F的大小和F的做功情况,下列说法正确的是( )
如图所示,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力F作用下,小球沿杆由底端匀速运动到顶端.已知小球与斜杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,则关于拉力F的大小和F的做功情况,下列说法正确的是( )
 如图所示,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力F作用下,小球沿杆由底端匀速运动到顶端.已知小球与斜杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,则关于拉力F的大小和F的做功情况,下列说法正确的是( )
如图所示,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力F作用下,小球沿杆由底端匀速运动到顶端.已知小球与斜杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,则关于拉力F的大小和F的做功情况,下列说法正确的是( )| A. | 当α=30°时,拉力F最小 | B. | 当α=30°时,拉力F做功最小 | ||
| C. | 当α=60°时,拉力F最小 | D. | 当α=60°时,拉力F做功最小 |
20. 如图所示,平面内有一菱形abcd,O点为两对角线交点,空间存在一匀强电场,方向与菱形所在平面平行,有一电子,若从a点运动到d点,电势能就会增加△E,若从d点运动到c点,电势能就会减小△E,则( )
如图所示,平面内有一菱形abcd,O点为两对角线交点,空间存在一匀强电场,方向与菱形所在平面平行,有一电子,若从a点运动到d点,电势能就会增加△E,若从d点运动到c点,电势能就会减小△E,则( )
 如图所示,平面内有一菱形abcd,O点为两对角线交点,空间存在一匀强电场,方向与菱形所在平面平行,有一电子,若从a点运动到d点,电势能就会增加△E,若从d点运动到c点,电势能就会减小△E,则( )
如图所示,平面内有一菱形abcd,O点为两对角线交点,空间存在一匀强电场,方向与菱形所在平面平行,有一电子,若从a点运动到d点,电势能就会增加△E,若从d点运动到c点,电势能就会减小△E,则( )| A. | 电场方向垂直于ac,并由b指向d | B. | 电场方向沿着ad,并由a指向d | ||
| C. | a点电势等于于c点电势 | D. | b点电势高于d点电势 |

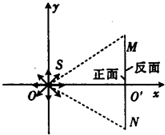 如图所示,在直角坐标系xOy的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的带正电的粒子,位于y轴的右侧有一垂直于z轴、长度为L的很薄的荧光屏MN,荧光屏正反面两侧均涂有荧光粉,MN与x轴交于点O′.已知三角形MNO为正三角形,放射源S射出的粒子质量为m,电荷量为q,速度大小为v,不计粒子的重力.
如图所示,在直角坐标系xOy的原点O处有一放射源S,放射源S在xOy平面内均匀发射速度大小相等的带正电的粒子,位于y轴的右侧有一垂直于z轴、长度为L的很薄的荧光屏MN,荧光屏正反面两侧均涂有荧光粉,MN与x轴交于点O′.已知三角形MNO为正三角形,放射源S射出的粒子质量为m,电荷量为q,速度大小为v,不计粒子的重力.