题目内容
9.若一条鱼儿正在水下10m处戏水,吐出的一个体积为1cm3的气泡.气泡内的气体视为理想气体,且气体质量保持不变,大气压强为P0=1.0×105Pa,g=10m/s2,湖水温度保持不变.(1)气泡在上升的过程中,气体吸热还是放热?请简述理由.
(2)气泡到达湖面时的体积多大?
分析 (1)湖水的温度不变,所以U等于0,又因为气体的体积逐渐增大,所以对外做功,W为负值,所以Q为正值,即气体吸收热量.
(2)由玻意耳定律求的体积
解答 解:(1)因为湖水的温度不变,所以U等于0,又因为气体的体积逐渐增大,所以对外做功,W为负值,所以Q为正值,即气体吸收热量,对外做功,内能不变.
(2)初态为:${P}_{1}={P}_{0}+ρgh=2×1{0}^{5}Pa$,${V}_{1}=1c{m}^{3}$
末态为:${P}_{2}=1×1{0}^{5}Pa$,T2
由玻意耳定律得:P1V1=P2V2
解得:${V}_{2}=2c{m}^{3}$
答:(1)气泡在上升的过程中,气体吸热1.
(2)气泡到达湖面时的体积2cm3
点评 题考查了理想气体状态方程和热力学第一定律的应用,难度中等.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
17.下列说法中正确的是( )
| A. | 初速度为v0、加速度为a的匀加速直线运动,可以看做是速度为v0的匀速直线运动和初速度为零、加速度为a的匀加速直线运动的合成 | |
| B. | 竖直下抛运动可以看做竖直向下的匀速直线运动和自由落体运动的合成 | |
| C. | 竖直上抛运动可看做竖直向上的匀速直线运动和自由落体运动的合成 | |
| D. | 以上说法都不对 |
4. 如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为l,两导轨间连有一电阻R,导轨平面与水平面的夹角为θ,在两虚线间的导轨上涂有薄绝缘涂层.匀强磁场的磁感应强度大小为B,方向与导轨平面垂直.质量为m的导体棒从h高度处由静止释放,在刚要滑到涂层处时恰好匀速运动.导体棒始终与导轨垂直且仅与涂层间有摩擦,动摩擦因数μ=tanθ,其他部分的电阻不计,重力加速度为g,下列说法正确的是( )
如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为l,两导轨间连有一电阻R,导轨平面与水平面的夹角为θ,在两虚线间的导轨上涂有薄绝缘涂层.匀强磁场的磁感应强度大小为B,方向与导轨平面垂直.质量为m的导体棒从h高度处由静止释放,在刚要滑到涂层处时恰好匀速运动.导体棒始终与导轨垂直且仅与涂层间有摩擦,动摩擦因数μ=tanθ,其他部分的电阻不计,重力加速度为g,下列说法正确的是( )
 如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为l,两导轨间连有一电阻R,导轨平面与水平面的夹角为θ,在两虚线间的导轨上涂有薄绝缘涂层.匀强磁场的磁感应强度大小为B,方向与导轨平面垂直.质量为m的导体棒从h高度处由静止释放,在刚要滑到涂层处时恰好匀速运动.导体棒始终与导轨垂直且仅与涂层间有摩擦,动摩擦因数μ=tanθ,其他部分的电阻不计,重力加速度为g,下列说法正确的是( )
如图所示,在匀强磁场中有一倾斜的平行金属导轨,导轨间距为l,两导轨间连有一电阻R,导轨平面与水平面的夹角为θ,在两虚线间的导轨上涂有薄绝缘涂层.匀强磁场的磁感应强度大小为B,方向与导轨平面垂直.质量为m的导体棒从h高度处由静止释放,在刚要滑到涂层处时恰好匀速运动.导体棒始终与导轨垂直且仅与涂层间有摩擦,动摩擦因数μ=tanθ,其他部分的电阻不计,重力加速度为g,下列说法正确的是( )| A. | 导体棒到达涂层前做加速度减小的加速运动 | |
| B. | 在涂层区导体棒做减速运动 | |
| C. | 导体棒到达底端的速度为$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$ | |
| D. | 整个运动过程中产生的焦耳热为mgh-$\frac{{m}^{3}{g}^{2}si{n}^{2}θ}{2{B}^{4}{L}^{4}}$ |
14. 如图所示,密度为ρ、边长为L的均匀立方体,表面光滑,静止在水平面上,并抵住一个小木桩.有风与水平方向成45°角斜向上吹到立方体的一个面上,产生压强为p,则使立方体刚要翻动的p的值为( )
如图所示,密度为ρ、边长为L的均匀立方体,表面光滑,静止在水平面上,并抵住一个小木桩.有风与水平方向成45°角斜向上吹到立方体的一个面上,产生压强为p,则使立方体刚要翻动的p的值为( )
 如图所示,密度为ρ、边长为L的均匀立方体,表面光滑,静止在水平面上,并抵住一个小木桩.有风与水平方向成45°角斜向上吹到立方体的一个面上,产生压强为p,则使立方体刚要翻动的p的值为( )
如图所示,密度为ρ、边长为L的均匀立方体,表面光滑,静止在水平面上,并抵住一个小木桩.有风与水平方向成45°角斜向上吹到立方体的一个面上,产生压强为p,则使立方体刚要翻动的p的值为( )| A. | $\sqrt{2}Lρg$ | B. | $\frac{\sqrt{2}Lρg}{3}$ | C. | Lρg | D. | $\frac{\sqrt{2}Lρg}{2}$ |
1.太空垃圾如人造卫星一样按一定的轨道绕地球飞行,若某大块太空垃圾在稀薄空气阻力的作用下,轨道半径逐渐变小.这个过程中,太空垃圾的( )
| A. | 动能逐渐减小 | B. | 向心加速度逐渐减小 | ||
| C. | 机械能逐渐减小 | D. | 运动周期逐渐减小 |
19.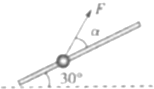 如图所示,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力F作用下,小球沿杆由底端匀速运动到顶端.已知小球与斜杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,则关于拉力F的大小和F的做功情况,下列说法正确的是( )
如图所示,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力F作用下,小球沿杆由底端匀速运动到顶端.已知小球与斜杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,则关于拉力F的大小和F的做功情况,下列说法正确的是( )
 如图所示,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力F作用下,小球沿杆由底端匀速运动到顶端.已知小球与斜杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,则关于拉力F的大小和F的做功情况,下列说法正确的是( )
如图所示,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力F作用下,小球沿杆由底端匀速运动到顶端.已知小球与斜杆之间的动摩擦因数为μ=$\frac{\sqrt{3}}{3}$,则关于拉力F的大小和F的做功情况,下列说法正确的是( )| A. | 当α=30°时,拉力F最小 | B. | 当α=30°时,拉力F做功最小 | ||
| C. | 当α=60°时,拉力F最小 | D. | 当α=60°时,拉力F做功最小 |
 如图所示,已知O、A、B、C为同一直线上的四点,OA间的距离l1,BC间的距离为l2,一物体自O点静止出发,沿此直线做匀加速运动,依次经过A、B、C三点,已知物体通过OA段与通过BC段所用的时间相等,求O与B的距离.
如图所示,已知O、A、B、C为同一直线上的四点,OA间的距离l1,BC间的距离为l2,一物体自O点静止出发,沿此直线做匀加速运动,依次经过A、B、C三点,已知物体通过OA段与通过BC段所用的时间相等,求O与B的距离.