题目内容
4.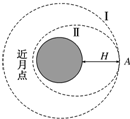 我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面H处的环月轨道Ⅰ上做匀速圆周运动,其运行的周期为T,随后“嫦娥三号”在该轨道上A点采取措施,降至近月点高度为h的椭圆轨道Ⅱ上,如图所示.若以R表示月球的半径,忽略月球自转及地球对卫星的影响.则下述判断正确的是( )
我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面H处的环月轨道Ⅰ上做匀速圆周运动,其运行的周期为T,随后“嫦娥三号”在该轨道上A点采取措施,降至近月点高度为h的椭圆轨道Ⅱ上,如图所示.若以R表示月球的半径,忽略月球自转及地球对卫星的影响.则下述判断正确的是( )| A. | “嫦娥三号”在环月轨道Ⅰ上需加速才能降至椭圆轨道Ⅱ | |
| B. | “嫦娥三号”在图中椭圆轨道Ⅱ上的周期为$\sqrt{\frac{{{{(2R+H+h)}^3}}}{{8{{(R+H)}^3}}}}T$ | |
| C. | 月球的质量为$\frac{{4{π^2}{{(R+H)}^3}}}{{G{T^2}}}$ | |
| D. | 月球的第一宇宙速度为$\frac{{2π\sqrt{R{{(R+H)}^3}}}}{TR}$ |
分析 根据万有引力提供圆周运动向心力求解月球的质量和第一宇宙速度,再根据开普勒行星运动定律求解椭圆轨道的周期.
解答 解:A、嫦娥三号在轨道I上运动,要使其沿椭圆轨道运动可知,嫦娥三号需做近心运动,故在轨道I上需要对嫦娥三号减速才可以沿轨道II运动,故A错误;
B、根据开普勒第三定律$\frac{{a}^{3}}{{T}^{2}}$=k,得在轨道I和轨道II上的周期满足:$\frac{{T}_{Ⅰ}}{{T}_{Ⅱ}}$=$\sqrt{[\frac{R+H}{\frac{1}{2}(2R+H+h)}]^{3}}$,TⅠ=T,解得:TⅡ=$\sqrt{\frac{{{{(2R+H+h)}^3}}}{{8{{(R+H)}^3}}}}T$.故B正确.
C、“嫦娥三号”在图中椭圆轨道Ⅰ上运行时,根据万有引力提供圆周运动向心力,有:
G$\frac{Mm}{(R+H)^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}$(R+H)
解得月球的质量为:M=$\frac{{4{π^2}{{(R+H)}^3}}}{{G{T^2}}}$,故C正确;
B、据 G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$得月球的第一宇宙速度为:v=$\sqrt{\frac{GM}{R}}$=$\frac{{2π\sqrt{R{{(R+H)}^3}}}}{TR}$,故D正确;
故选:BCD
点评 解决本题的关键是抓住万有引力提供圆周运动向心力和开普勒行星运动定律,掌握基础知识是解题的主要入手点.

练习册系列答案
相关题目
7.假设地球是一半径为R,质量分布均匀的球体.已知质量分布均匀的球壳对壳内物体引力为零,有人设想要打穿地球从中国建立一条通过地心的孔径大小可忽略的光滑隧道直达巴西.如只考虑物体间的万有引力,则从隧道口抛下一物体,物体的加速度( )
| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
19.下列说法不正确的有( )
| A. | 伽利略研究自由落体运动时,由于物体下落时间太短,不易测量,因此采用了“冲淡重力”的方法来测量时间,然后再把得出的结论合理外推 | |
| B. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法 | |
| C. | 牛顿运动定律都可以用实验直接验证 | |
| D. | 验证力的平行四边形实验中,采用了等效替代法 |
9. 伽利略在《两种新科学的对话》一书中,提出猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还实验验证了该猜想.某小组学生依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.实验操作步骤如下:
伽利略在《两种新科学的对话》一书中,提出猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还实验验证了该猜想.某小组学生依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.实验操作步骤如下:
①让滑块从离挡板某一距离L处由静止沿某一倾角θ的斜面下滑,并同时打开固定高度装置中的阀门,使水箱中的水流到量筒中;
②当滑块碰到挡板的同时关闭水箱阀门(假设水流出时均匀稳定);
③记录下量筒收集的水量V;
④改变滑块起始位置离挡板的距离,重复以上操作;
⑤测得的数据见表格:
①该实验利用量筒中收集的水量来表示C.(填序号)
A.水箱中水的体积 B.水从水箱中流出的速度 C.滑块下滑的时间 D.滑块下滑的位移
②小组同学漏填了第3组数据,实验正常,你估计这组水量V=74mL.
(3)若保持倾角θ不变,增大滑块质量,则相同的L,水量V将不变(填“增大”“不变”或“减小”);若保持滑块质量不变,增大倾角θ,则相同的L,水量V将减少.(填“增大”“不变”或“减小”)
 伽利略在《两种新科学的对话》一书中,提出猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还实验验证了该猜想.某小组学生依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.实验操作步骤如下:
伽利略在《两种新科学的对话》一书中,提出猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还实验验证了该猜想.某小组学生依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.实验操作步骤如下:①让滑块从离挡板某一距离L处由静止沿某一倾角θ的斜面下滑,并同时打开固定高度装置中的阀门,使水箱中的水流到量筒中;
②当滑块碰到挡板的同时关闭水箱阀门(假设水流出时均匀稳定);
③记录下量筒收集的水量V;
④改变滑块起始位置离挡板的距离,重复以上操作;
⑤测得的数据见表格:
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| L(m) | 4.5 | 3.9 | 3.0 | 2.1 | 1.5 | 0.9 |
| V(mL) | 90 | 84 | 62 | 52 | 40 |
A.水箱中水的体积 B.水从水箱中流出的速度 C.滑块下滑的时间 D.滑块下滑的位移
②小组同学漏填了第3组数据,实验正常,你估计这组水量V=74mL.
(3)若保持倾角θ不变,增大滑块质量,则相同的L,水量V将不变(填“增大”“不变”或“减小”);若保持滑块质量不变,增大倾角θ,则相同的L,水量V将减少.(填“增大”“不变”或“减小”)
16. 如图所示,质量为m的木块在质量为M的长木板上向右滑行,木块同时受到水平向右的力F作用,长木板处于静止状态.已知木块和长木板之间的动摩擦因数为μ1,木板与地面之间的动摩擦因数为μ2,下列说法正确的是( )
如图所示,质量为m的木块在质量为M的长木板上向右滑行,木块同时受到水平向右的力F作用,长木板处于静止状态.已知木块和长木板之间的动摩擦因数为μ1,木板与地面之间的动摩擦因数为μ2,下列说法正确的是( )
 如图所示,质量为m的木块在质量为M的长木板上向右滑行,木块同时受到水平向右的力F作用,长木板处于静止状态.已知木块和长木板之间的动摩擦因数为μ1,木板与地面之间的动摩擦因数为μ2,下列说法正确的是( )
如图所示,质量为m的木块在质量为M的长木板上向右滑行,木块同时受到水平向右的力F作用,长木板处于静止状态.已知木块和长木板之间的动摩擦因数为μ1,木板与地面之间的动摩擦因数为μ2,下列说法正确的是( )| A. | 木板受到的摩擦力可能是μ1mg | |
| B. | 木块受到摩擦力一定是μ1mg | |
| C. | 当F>μ2(m+M)g时,木板与木块之间发生相对运动 | |
| D. | 无论怎样改变F的大小,木板都不会运动 |
13. 如图所示,在水平面上一轻质弹簧竖直放置,在它正上方一小球自由落下,不空气阻力,从小球接触弹簧到速度减为零的过程中 ( )
如图所示,在水平面上一轻质弹簧竖直放置,在它正上方一小球自由落下,不空气阻力,从小球接触弹簧到速度减为零的过程中 ( )
 如图所示,在水平面上一轻质弹簧竖直放置,在它正上方一小球自由落下,不空气阻力,从小球接触弹簧到速度减为零的过程中 ( )
如图所示,在水平面上一轻质弹簧竖直放置,在它正上方一小球自由落下,不空气阻力,从小球接触弹簧到速度减为零的过程中 ( )| A. | 小球的动能不断减小 | B. | 小球所受的合力不断增大 | ||
| C. | 弹簧的弹性势能不断增大 | D. | 小球的机械能守恒 |
 如图所示,光滑、半圆形轨道竖直放置,轨道半径R=80cm,其底部与粗糙、水平轨道相接,连接点为P,一小球A以一定的初速度沿水平轨道向左运动,测得小球A经过N点时的速度vN=8m/s,小球A经过水平轨道后沿圆轨道的内壁运动到最高点M,测得经过M点时对轨道的压力为0.5N,小球A的质量m=50g,重力加速度度g=10m/s2.求:
如图所示,光滑、半圆形轨道竖直放置,轨道半径R=80cm,其底部与粗糙、水平轨道相接,连接点为P,一小球A以一定的初速度沿水平轨道向左运动,测得小球A经过N点时的速度vN=8m/s,小球A经过水平轨道后沿圆轨道的内壁运动到最高点M,测得经过M点时对轨道的压力为0.5N,小球A的质量m=50g,重力加速度度g=10m/s2.求: 如图所示,一导热性能良好的容器水平放置,两端是直径不同的两个圆筒,里面各有一个活塞,其横截面积分别为SA=10cm2和SB=4cm2,质量分别是MA=6kg,MB=4kg.它们之间用一质量不计的轻质细杆相连.两活塞可在筒内无摩擦活动,但不漏气.在气温是-23℃时,用销子M把B拴住,并把阀门K打开,使容器和大气相通,随后关闭K,此时两活塞间气体体积是300cm3,当气温升到了T=300K时求(设大气压强为1.0×105Pa不变,容器内气体温度始终和外界气温相同):
如图所示,一导热性能良好的容器水平放置,两端是直径不同的两个圆筒,里面各有一个活塞,其横截面积分别为SA=10cm2和SB=4cm2,质量分别是MA=6kg,MB=4kg.它们之间用一质量不计的轻质细杆相连.两活塞可在筒内无摩擦活动,但不漏气.在气温是-23℃时,用销子M把B拴住,并把阀门K打开,使容器和大气相通,随后关闭K,此时两活塞间气体体积是300cm3,当气温升到了T=300K时求(设大气压强为1.0×105Pa不变,容器内气体温度始终和外界气温相同):