题目内容
9. 伽利略在《两种新科学的对话》一书中,提出猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还实验验证了该猜想.某小组学生依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.实验操作步骤如下:
伽利略在《两种新科学的对话》一书中,提出猜想:物体沿斜面下滑是一种匀变速直线运动,同时他还实验验证了该猜想.某小组学生依据伽利略描述的实验方案,设计了如图所示的装置,探究物体沿斜面下滑是否做匀变速直线运动.实验操作步骤如下:①让滑块从离挡板某一距离L处由静止沿某一倾角θ的斜面下滑,并同时打开固定高度装置中的阀门,使水箱中的水流到量筒中;
②当滑块碰到挡板的同时关闭水箱阀门(假设水流出时均匀稳定);
③记录下量筒收集的水量V;
④改变滑块起始位置离挡板的距离,重复以上操作;
⑤测得的数据见表格:
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| L(m) | 4.5 | 3.9 | 3.0 | 2.1 | 1.5 | 0.9 |
| V(mL) | 90 | 84 | 62 | 52 | 40 |
A.水箱中水的体积 B.水从水箱中流出的速度 C.滑块下滑的时间 D.滑块下滑的位移
②小组同学漏填了第3组数据,实验正常,你估计这组水量V=74mL.
(3)若保持倾角θ不变,增大滑块质量,则相同的L,水量V将不变(填“增大”“不变”或“减小”);若保持滑块质量不变,增大倾角θ,则相同的L,水量V将减少.(填“增大”“不变”或“减小”)
分析 (1)解答的关键是明确该实验的实验原理,初速度为零的匀变速运动,位移与时间的二次方成正比,由于水是均匀稳定的流出,水的体积和时间成正比,所以该实验只要验证位移与体积的二次方是否成正比,就可验证该运动是否匀变速直线运动.
(2)(3)根据初速度为零初速度为零的匀变速运动,位移与时间的二次方成正比,由于水是均匀稳定的流出,水的体积和时间成正比,由此可以求出下滑位移s与水量体积之间的关系,以及水量的变化情况.
解答 解:(1)关于初速度为零的匀变速运动,位移与时间的二次方成正比,由于水是均匀稳定的流出,水的体积和时间成正比,所以量筒中收集的水量可以间接的测量时间.
故选:C.
(2)该运动是匀变速直线运动,位移与时间的二次方是成正比,即位移与体积的二次方是成正比,即L=kV2.
根据1、3组数据可得:
L1=kv12
L3=kv32
小组同学漏填了第3组数据,实验正常,由此解得水量为:V3≈74mL;
(3)若保持倾角θ不变,增大滑块质量,物体的加速度不变,则相同的s,水量V将不变,若保持滑块质量不变,增大倾角θ,加速度将增大,则相同的s,时间减小,水量V将减少.
故答案为:(1)C;(2)74;(3)不变,减少
点评 解决该问题的关键是明确实验原理,根据流入量筒水的量与时间成正比,将时间问题转化为为水量问题即可求解,本题是考查学生创新能力的好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.关于功与能的认识,下列说法中正确的是( )
| A. | 当重力对物体做正功时,物体的重力势能一定减少 | |
| B. | 重力做功的多少与参考平面的选取有关 | |
| C. | 物体受拉力和重力的作用下向上运动,拉力做功10J,但物体重力势能的增加量有可能不是10J | |
| D. | 对于质量一定的物体,速度发生变化,则其动能一定发生变化 |
17.在公式d=$\frac{V}{S}$计算油膜分子大小时,式中V的物理意义是( )
| A. | 指1mL的油酸溶液的体积 | |
| B. | 指一滴油酸溶液的体积 | |
| C. | 指一滴油酸溶液中所含纯油酸的体积 | |
| D. | 指一滴油酸溶液中酒精的体积 |
4.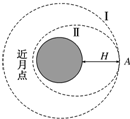 我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面H处的环月轨道Ⅰ上做匀速圆周运动,其运行的周期为T,随后“嫦娥三号”在该轨道上A点采取措施,降至近月点高度为h的椭圆轨道Ⅱ上,如图所示.若以R表示月球的半径,忽略月球自转及地球对卫星的影响.则下述判断正确的是( )
我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面H处的环月轨道Ⅰ上做匀速圆周运动,其运行的周期为T,随后“嫦娥三号”在该轨道上A点采取措施,降至近月点高度为h的椭圆轨道Ⅱ上,如图所示.若以R表示月球的半径,忽略月球自转及地球对卫星的影响.则下述判断正确的是( )
 我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面H处的环月轨道Ⅰ上做匀速圆周运动,其运行的周期为T,随后“嫦娥三号”在该轨道上A点采取措施,降至近月点高度为h的椭圆轨道Ⅱ上,如图所示.若以R表示月球的半径,忽略月球自转及地球对卫星的影响.则下述判断正确的是( )
我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面H处的环月轨道Ⅰ上做匀速圆周运动,其运行的周期为T,随后“嫦娥三号”在该轨道上A点采取措施,降至近月点高度为h的椭圆轨道Ⅱ上,如图所示.若以R表示月球的半径,忽略月球自转及地球对卫星的影响.则下述判断正确的是( )| A. | “嫦娥三号”在环月轨道Ⅰ上需加速才能降至椭圆轨道Ⅱ | |
| B. | “嫦娥三号”在图中椭圆轨道Ⅱ上的周期为$\sqrt{\frac{{{{(2R+H+h)}^3}}}{{8{{(R+H)}^3}}}}T$ | |
| C. | 月球的质量为$\frac{{4{π^2}{{(R+H)}^3}}}{{G{T^2}}}$ | |
| D. | 月球的第一宇宙速度为$\frac{{2π\sqrt{R{{(R+H)}^3}}}}{TR}$ |
14. 如图,一半径为R的半圆形轨道竖直固定放置,轨道两等高、质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为1.5mg,重力加速度大小为g.质点自P滑到Q的过程中,克服摩擦力所做的功为( )
如图,一半径为R的半圆形轨道竖直固定放置,轨道两等高、质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为1.5mg,重力加速度大小为g.质点自P滑到Q的过程中,克服摩擦力所做的功为( )
 如图,一半径为R的半圆形轨道竖直固定放置,轨道两等高、质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为1.5mg,重力加速度大小为g.质点自P滑到Q的过程中,克服摩擦力所做的功为( )
如图,一半径为R的半圆形轨道竖直固定放置,轨道两等高、质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为1.5mg,重力加速度大小为g.质点自P滑到Q的过程中,克服摩擦力所做的功为( )| A. | $\frac{1}{2}$mgR | B. | $\frac{1}{4}$mgR | C. | $\frac{3}{4}$mgR | D. | $\frac{π}{2}$mgR |
19. 如图所示,将打点计时器固定在铁架台上,用重物带动纸带从静止开始自由下落,利用此装置可验证机械能守恒定律.实验中需要测量物体由静止开始自由下落到某点时的瞬时速度v和下落高度h. 某同学对实验得到的纸带,设计了以下四种测量方案,这些方案中正确的是( )
如图所示,将打点计时器固定在铁架台上,用重物带动纸带从静止开始自由下落,利用此装置可验证机械能守恒定律.实验中需要测量物体由静止开始自由下落到某点时的瞬时速度v和下落高度h. 某同学对实验得到的纸带,设计了以下四种测量方案,这些方案中正确的是( )
 如图所示,将打点计时器固定在铁架台上,用重物带动纸带从静止开始自由下落,利用此装置可验证机械能守恒定律.实验中需要测量物体由静止开始自由下落到某点时的瞬时速度v和下落高度h. 某同学对实验得到的纸带,设计了以下四种测量方案,这些方案中正确的是( )
如图所示,将打点计时器固定在铁架台上,用重物带动纸带从静止开始自由下落,利用此装置可验证机械能守恒定律.实验中需要测量物体由静止开始自由下落到某点时的瞬时速度v和下落高度h. 某同学对实验得到的纸带,设计了以下四种测量方案,这些方案中正确的是( )| A. | 用刻度尺测出物体下落高度h,由打点间隔数算出下落时间t,通过v=gt计算出瞬时速度v | |
| B. | 用刻度尺测出物体下落的高度h,并通过v=$\sqrt{2gh}$ 计算出瞬时速度v | |
| C. | 根据做匀变速直线运动时,纸带上某点的瞬时速度等于这点前后相邻两点间的平均速度,测算出瞬时速度v,并通过h=$\frac{{v}^{2}}{2g}$ 计算得出高度h | |
| D. | 用刻度尺测出物体下落的高度h,根据做匀变速直线运动时,纸带上某点的瞬时速度等于这点前后相邻两点间的平均速度,测算出瞬时速度v |
 如图是上海中心大厦,小明乘坐大厦快速电梯,从底层到达第119层观光平台仅用时55s.若电梯先以加速度a1做匀加速运动,达到最大速度18m/s,然后以最大速度匀速运动,最后以加速度a2做匀减速运动恰好到达观光平台.假定观光平台高度为549m.
如图是上海中心大厦,小明乘坐大厦快速电梯,从底层到达第119层观光平台仅用时55s.若电梯先以加速度a1做匀加速运动,达到最大速度18m/s,然后以最大速度匀速运动,最后以加速度a2做匀减速运动恰好到达观光平台.假定观光平台高度为549m. 如图所示,传送带保持2m/s的速度顺时针转动.现将一质量m=0.5kg的煤块轻轻地放在传送带的a点上,a、b间的距离L=5m,煤块从a点先匀加速后匀速运动到b点,所经历的时间为3s,求:
如图所示,传送带保持2m/s的速度顺时针转动.现将一质量m=0.5kg的煤块轻轻地放在传送带的a点上,a、b间的距离L=5m,煤块从a点先匀加速后匀速运动到b点,所经历的时间为3s,求: